Read the paper Download the datasets
Over the past few years, adversarial examples – or inputs that have been slightly perturbed by an adversary to cause unintended behavior in machine learning systems – have received significant attention in the machine learning community (for more background, read our introduction to adversarial examples here). There has been much work on training models that are not vulnerable to adversarial examples (in previous posts, we discussed methods for training robust models: part 1, part 2, but all this research does not really confront the fundamental question: why do these adversarial examples arise in the first place?
So far, the prevailing view has been that adversarial examples stem from “quirks” of the models that will eventually disappear once we make enough progress towards better training algorithms and larger scale data collection. Common views include adversarial examples being either a consequence of the input space being high-dimensional (e.g. here) or attributed to finite-sample phenomena (e.g. here or here).
Today we will discuss our recent work that provides a new perspective on the reasons for adversarial examples arise. However, before we dive into the details, let us first tell you a short story:
A Planet called Erm
Our tale begins on Erm, a distant planet inhabited by members of an ancient alien race known as Nets. The Nets are a strange species; each individual’s place in the social hierarchy is determined by their ability to classify bizarre 32-by-32 pixel images (which are meaningless to the Nets) into ten completely arbitrary categories. These images are drawn from a top-secret dataset, See-Far—outside of looking at those curious pixelated images, the Nets live their lives totally blind.
As Nets grow older and wiser they begin to discover more and more tell-tale patterns in See-Far. Each new pattern that an alien discovers helps them classify the dataset even more accurately. Due to the immense societal value of increased classification accuracy, the aliens have names for the most predictive image patterns:
The most powerful aliens were remarkably adept at spotting patterns, and thus were extremely sensitive to their presence in See-Far images.
Somehow (perhaps looking for See-Far classification tips), some of the aliens obtain access to a human-written machine learning paper. One figure in particular caught the aliens’ eye:

The figure was relatively simple, they thought: on the left was a “2”, in the middle there was a GAB pattern, which was known to indicate “4”—unsurprisingly, adding a GAB to the image on the left resulted in a new image, which looked (to the Nets) exactly like an image corresponding to the “4” category.
The Nets could not understand why, according to the paper, the original and final images, being completely different, should be identically classified. Confused, the Nets flipped on through the manuscript, wondering what other useful patterns humans were oblivious to$\ldots$
What we can learn from Erm
As the names may suggest, this story is not merely one of aliens and their curious social constructs: the way Nets develop is reminiscent of how we train machine learning models. In particular, we maximize accuracy without incorporating much prior context about classified classes, the physical world, or other human-related concepts. The result in the story is that the aliens are able to realize that what humans think of as meaningless adversarial perturbation are actually patterns crucial to See-Far classification. The tale of the Nets should thus make us wonder:
Are adversarial perturbations really unnatural and meaningless?
A simple experiment
To investigate this issue, let us first perform a simple experiment:
- We start with an image from the training set of a standard dataset (e.g. CIFAR10):
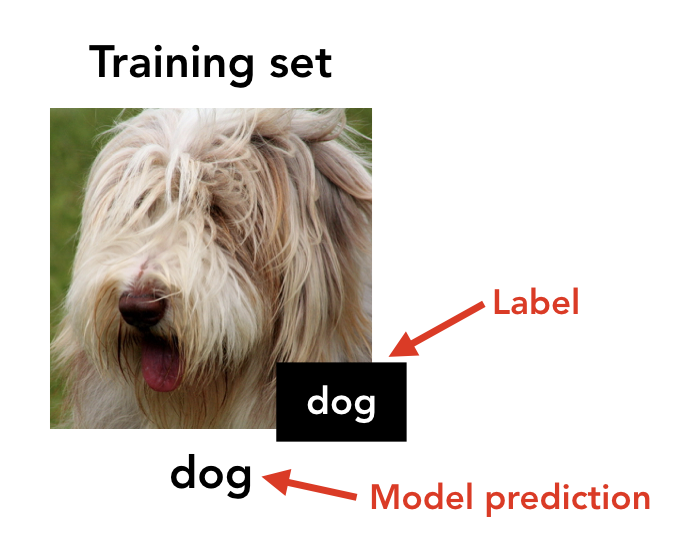
- We synthesize a targeted adversarial example (on a standard pre-trained model) from each (x, y) towards the “next” class y+1 (or 0, if y is the last class):
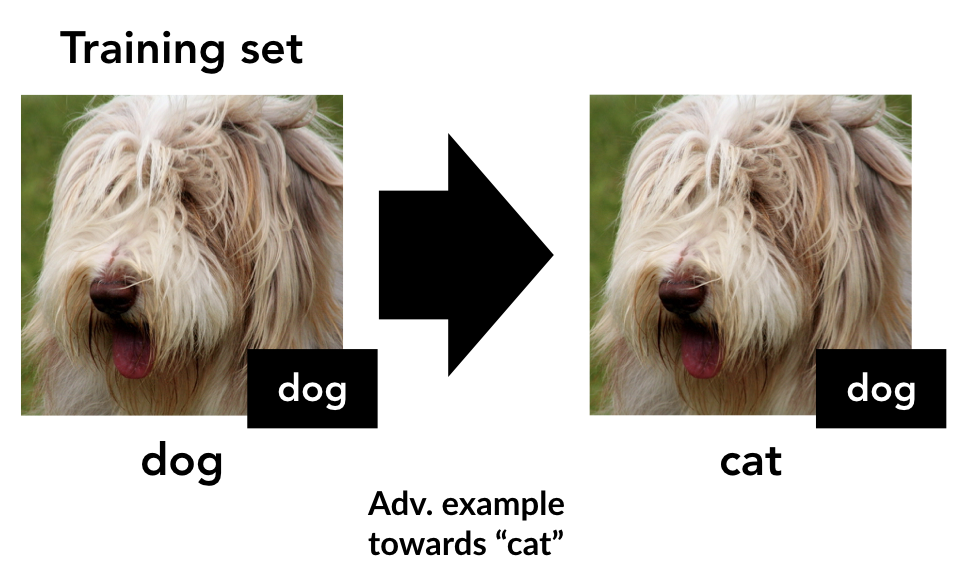
- We then construct a new training set, by labeling these adversarial examples with their corresponding target class:

Now, the resulting training set is imperceptibly perturbed from the original, but the labels have been changed—as such, it looks completely mislabeled to a human. In fact, the mislabelings are even consistent with a “permuted” hypothesis (i.e. every dog is labeled as a cat, every cat as a bird, etc.).
We train a new classifier (not necessarily with the same architecture as the first) on the “mislabeled dataset.” How will this classifier perform on the original (unaltered) test set (i.e. the standard CIFAR-10 test set)?
Remarkably, we find that the resulting classifier actually has moderate accuracy (e.g. 44% for CIFAR)! This is despite the fact that training inputs are associated with their “true” labels solely through imperceptible perturbations, and are associated with a different (now incorrect) label matching through all visible features.
What’s going on here?
Our Conceptual Model for Adversarial Examples
The experiment we just described establishes adversarial perturbations of standard models as patterns predictive of the target class in a well-generalizing sense. That is, adversarial perturbations in the training set alone allowed moderately accurate predictions on the test set. In this light, one might wonder: perhaps these patterns are not fundamentally different from what humans use to classify images (e.g. ears, whiskers, snouts)! This is precisely our hypothesis—there exist a variety of features of the input that are predictive of the label, and only some of these are perceptible to humans.
More precisely, we posit that predictive features of the data can be split into “robust” and “non-robust” features. Robust features correspond to patterns that are predictive of the true label even when adversarially perturbed (e.g. the presence of “fur” in an image) under some pre-defined (and crucially human-defined) perturbation set, e.g. the $\ell_2$ ball. Conversely, non-robust features correspond to patterns that while predictive, can be “flipped” by an adversary within a pre-defined perturbation set to be indicate a wrong class (see our paper for a formal definition).
Since we always only consider perturbation sets that do not affect human classification performance, we expect humans to rely solely on robust features. However, when the goal is maximizing (standard) test-set accuracy, non-robust features can be just as useful as robust ones–in fact, the two types of features are completely interchangeable. This is illustrated in the following figure:
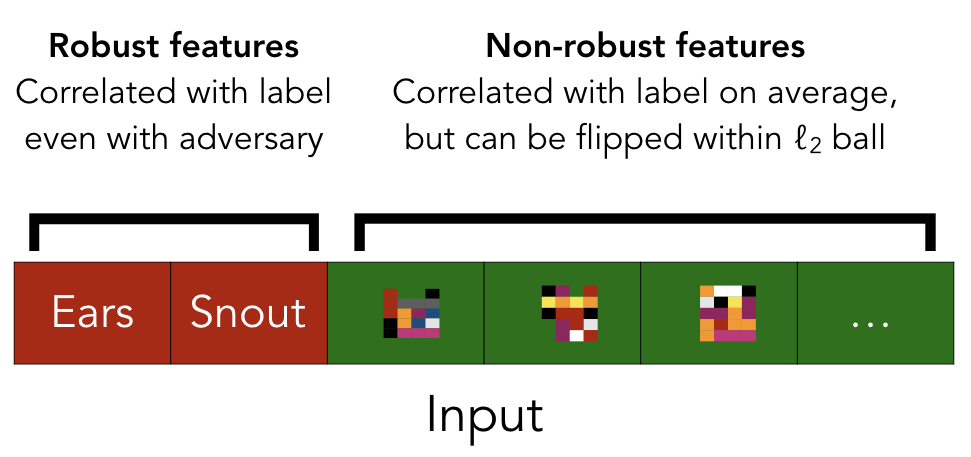
From this perspective, our experiment describes something quite simple. In the original training set, both the robust and non-robust features of the input are predictive of the label. When we make a small adversarial perturbation, we cannot significantly affect the robust features (essentially by definition), but we can still flip non-robust features. For instance, every dog image now retains the robust features of a dog (and thus appears to us to be a dog), but has non-robust features of a cat. After the training set is relabelled, we make it so that the robust features actually point in the wrong direction (i.e. the pictures with robust “dog” features are labeled as cats) and hence only the non-robust features actually provide correct guidance for generalization.
In summary, both robust and non-robust features are predictive on the training set, but only non-robust features will yield generalization to the original test set:
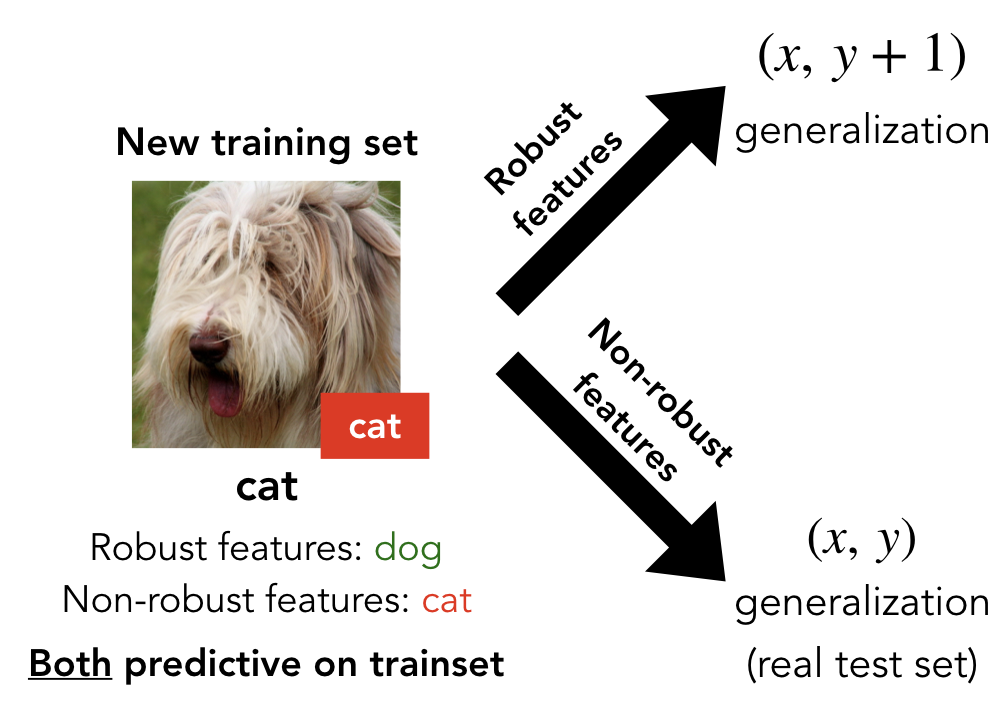
Thus, the fact that models trained on this dataset actually generalize to the standard test set indicates that (a) non-robust features exist and are sufficient for good generalization, and (b) deep neural networks indeed rely on these non-robust features, even in the presence of predictive robust features.
Do Robust Models Learn Robust Features?
Our experiments establish that adversarial perturbations are not meaningless artifacts but actually correspond directly to perturbing features that are crucial to generalization. At the same time, our blog posts about adversarial examples (here and here) showed that by using robust optimization, we can get models that are more robust to adversarial examples.
So a natural question to ask is: can we verify that robust models actually rely on robust features? To test this, we establish a methodology for restricting (in a best-effort sense) inputs to only the features a model is sensitive to (for deep neural networks, features correspond to the penultimate layer activations). Using this method, we create a new training set that is restricted to only contain the features that an already-trained robust model utilizes:

We then train a model on the resulting dataset without adversarial training and find that the resulting model has non-trivial accuracy and robustness! This is in stark contrast to training on the standard training set which leads to models that are accurate yet completely brittle.
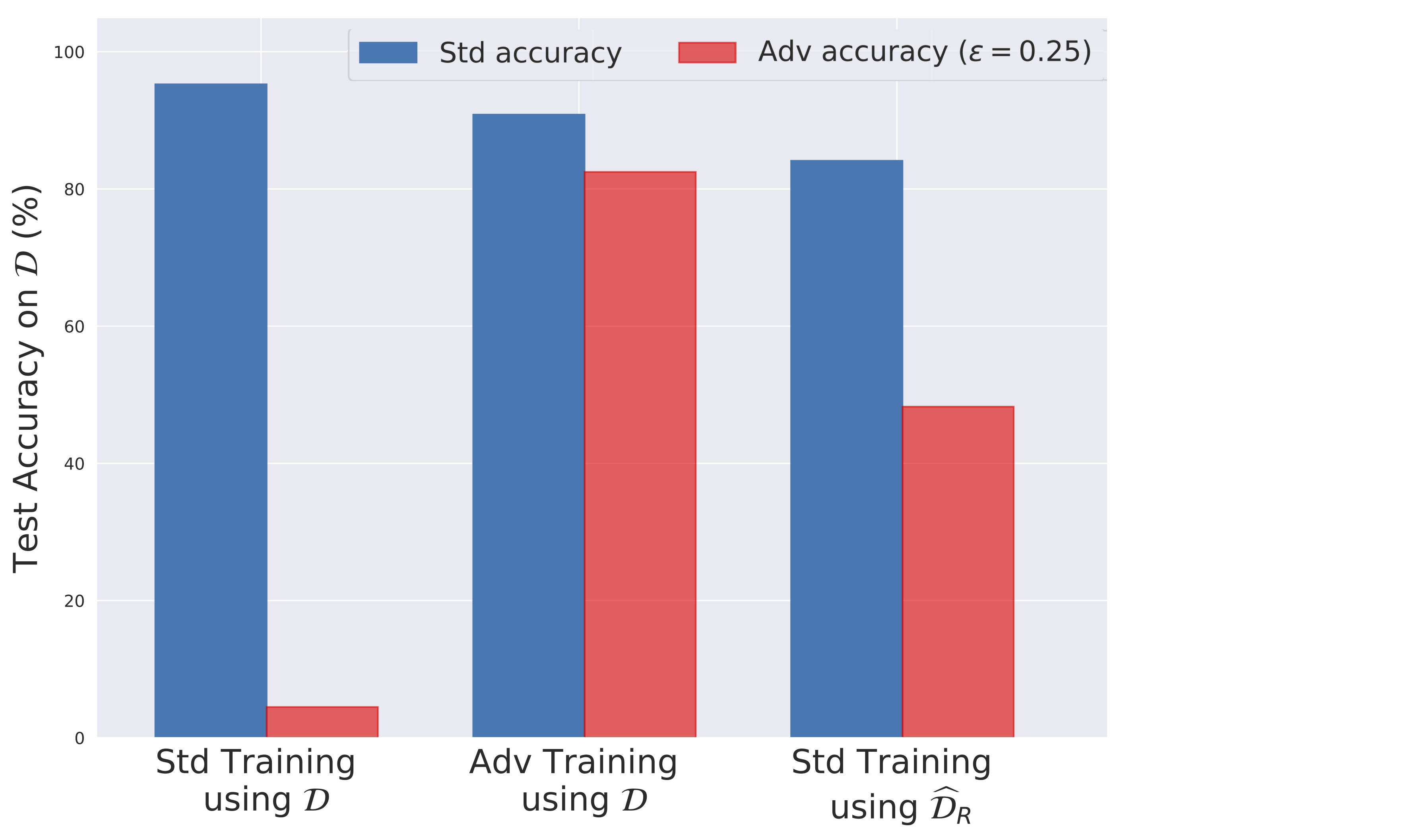
Left: training normally on CIFAR-10 ($\mathcal{D}$)
Middle: training adversarially on CIFAR-10 ($\mathcal{D}$)
Right: training normally on constructed dataset ($\widehat{\mathcal{D}}_R$)
Our results thus indicate that robustness (and in turn non-robustness) can in fact arise as a property of the dataset itself. In particular, when we remove non-robust features from the original training set, we can get robust models just via standard (non-adversarial) training. This is further evidence that adversarial examples arise as a result of non-robust features and are not necessarily tied to the standard training framework.
Transferability
An immediate consequence of this change in perspective is that the transferability of adversarial examples (the thus-far mysterious phenomenon that perturbations for one model are often adversarial for others) no longer requires a separate explanation. Specifically, now that we view adversarial vulnerability as a direct product of the features derived from the dataset (as opposed to quirks in the training of individual models), we would expect similarly expressive models to be able to find and use these features to improve their classification accuracy too.
To further explore this idea, we study how the tendency of different architectures to learning similar non-robust features relates to the transferability of adversarial examples between them:
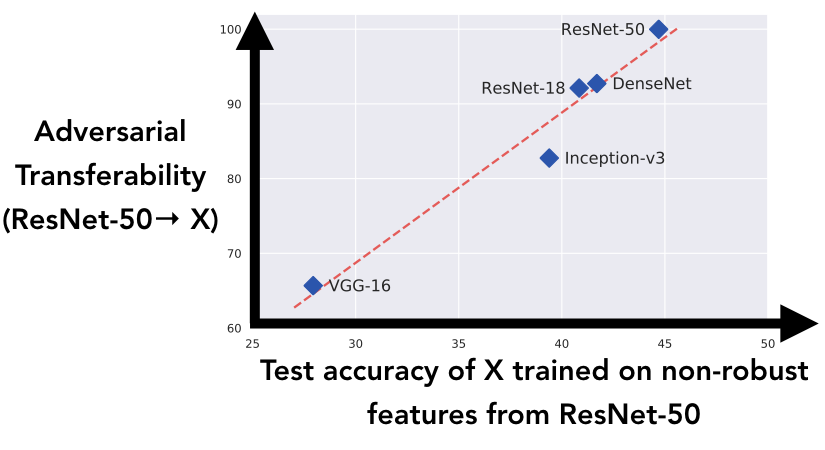 In the above, we generate the dataset that we described in our very first experiment (a training set of adversarial examples labeled with the target class), using a ResNet-50 to construct the adversarial examples. We can think of the resulting dataset as having all of the ResNet-50’s non-robust features “flipped” to the target class. We then train the five architectures shown above on this dataset, and record their generalization performance on the true test set: this corresponds to how well the architecture is able to generalize using only the non-robust features from a ResNet-50.
In the above, we generate the dataset that we described in our very first experiment (a training set of adversarial examples labeled with the target class), using a ResNet-50 to construct the adversarial examples. We can think of the resulting dataset as having all of the ResNet-50’s non-robust features “flipped” to the target class. We then train the five architectures shown above on this dataset, and record their generalization performance on the true test set: this corresponds to how well the architecture is able to generalize using only the non-robust features from a ResNet-50.
When we analyze the results we see that, as our new view of adversarial examples suggests, models’ ability to pick up the non-robust features introduced by the ResNet-50 correlates extremely well with the adversarial transferability from ResNet-50 to standard models of each architecture.
Implications
Our discussion and experiments establish adversarial examples as a purely human-centric phenomenon. From the perspective of classification performance there is no reason for a model to prefer robust over non-robust features. After all, the notion of robustness is human-specified. Hence, if we want our models to rely mostly on robust features we need to explicitly account for that by incorporating priors into architecture or training process. From that perspective, adversarial training (and more broadly robust optimization) can be thought of as a tool to incorporate desired invariances into the learned model. For example, robust training can be viewed as attempting to undermine the predictiveness of non-robust features by constantly “flipping” them, and thus steering the trained model away from relying on them.
At the same time, the reliance of standard models on non-robust (and hence incomprehensible to humans) features needs to be accounted for when designing interpretability methods. In particular, any “explanation” of a standardly trained model’s prediction should either highlight such non-robust features (and hence not be fully human-meaningful) or hide them (and hence not be fully faithful to the model’s decision process). Therefore, if we want interpretability methods that are both human-meaningful and faithful, resorting only to post-training processing is fundamentally insufficient: one needs to intervene at training time.
More in the Paper
In our paper, we also describe a precise framework for discussing robust and non-robust features, further experiments corroborating our hypothesis, and a theoretical model under which we can study the dynamics of robust training in the presence of non-robust features.
