Paper
Data
What drives machine learning (ML) models’ predictions?
This question is rarely an easy one to answer. On one hand, we know that predictions are a product of training data and learning algorithms. On the other hand, it is often hard to characterize exactly how these two elements interact.
In our latest work, we introduce datamodels—a step towards acquiring a more fine-grained understanding of how learning algorithms use training data to make predictions. This post introduces the datamodeling framework, describes its simplest, linear instantiation, and illustrates its success in modeling data-to-prediction mapping for deep neural networks. Our future posts will tour through some of the applications of the datamodeling framework that we are most excited about.
What is a datamodel?
In the standard machine learning setup, we have both a learning algorithm (say, stochastic gradient descent applied to a deep neural network) and a training set to learn from (say, the CIFAR-10 training set).
Now, suppose that we want to evaluate model behavior on a specific input \(x\). For example, \(x\) might be one of the following input-label pairs from the CIFAR-10 test set:
 "horse"
"horse"
 "dog"
"dog"
 "boat"
"boat"
 "firetruck"
"firetruck"
A natural question that might arise in this context is: for such an example \(x\), how does the learning algorithm use the training data to arrive at its prediction? Answering this question is difficult—think of the underlying complexity stemming from training a deep neural network using thousands of stochastic gradient descent (SGD) steps.
Our datamodeling framework is motivated exactly by this challenge. Specifically, the goal of datamodeling is to bypass that complexity of model training entirely, and instead find a simple function that directly maps training data to predictions. So, roughly speaking, a datamodel for a specific example of interest \(x\) is a function \(g(S’)\) that takes as input any subset \(S’\) of the original training \(S\), and as output predicts the outcome of training a model on \(S’\) and then evaluating on \(x\).
For the visual learners out there, datamodels have the following interface:
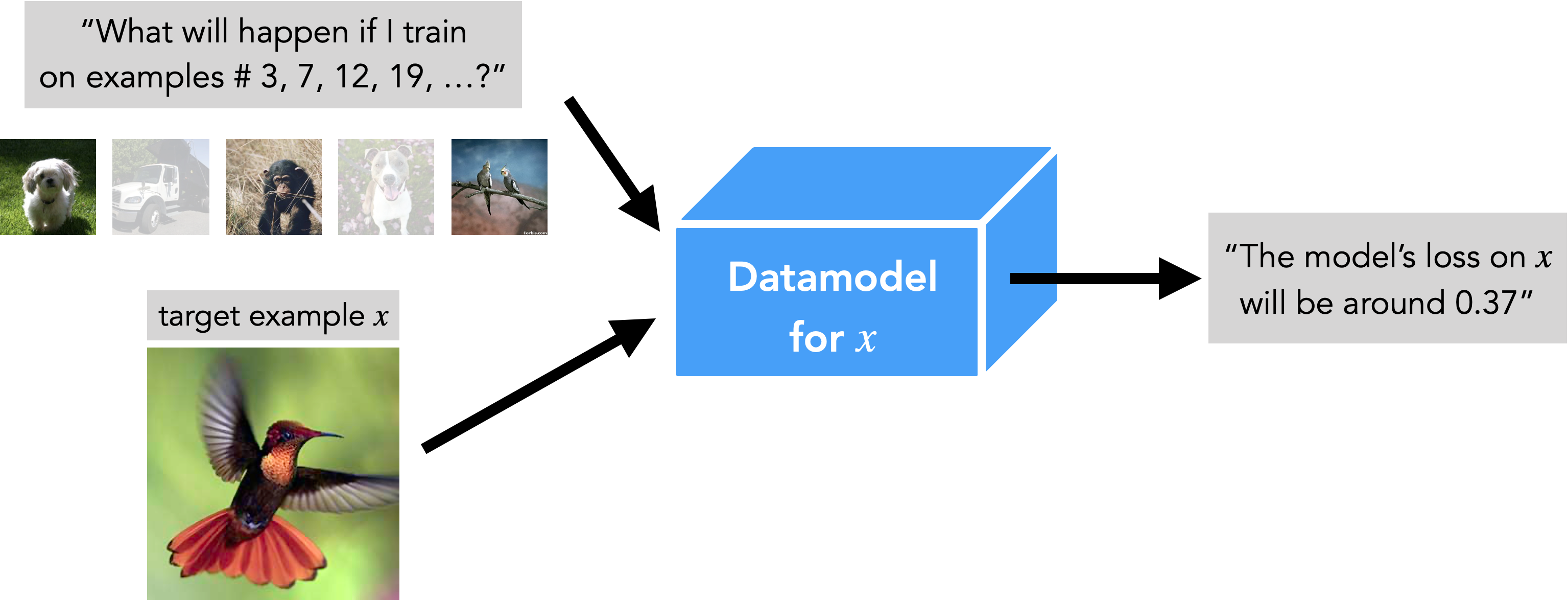
The hope is to find datamodels that are simple enough to analyze directly, yet accurate enough to faithfully capture model behavior. We then can use such datamodels to gain insight into how the algorithm and data combine through the lens of the training dynamics (but without having to analyze that dynamics directly).
At first glance, this of task of predicting the output of a learning algorithm trained on different subsets of the original training set does not appear any easier than analyzing the learning algorithm on that original training set—in fact, it might seem even harder. At the very least, one would expect that any function approximating such a learning algorithm would need to be rather complicated. It turns out, however, that a (very) simple instantiation of datamodels—as linear functions—is already expressive enough to accurately capture the intended mapping, even for real-world deep neural networks!
Linear datamodels for deep classifiers
How exactly do we formulate linear datamodels? We represent each subset \(S’\) of the training set as an indicator vector \(\mathbf{1}_{S’}\), and then have our datamodel \(g_\theta\) map such indicator vectors to scalars. Specifically, we parameterize linear datamodels as:
\[g_\theta(S’) = \mathbf{1}_{S’}^\top \theta + \theta_0,\]where \(\theta\) are our model’s parameters.
Estimating linear datamodels
Now, how do we actually select parameters \(\theta\) for such a linear datamodel? Recall that our goal is to find a \(\theta\) such that our linear datamodel satisfies:
Our idea is to frame this task as a supervised learning problem in which we infer \(g_\theta\) from “input-label pairs.” Here, each of these pairs consists of a specific training subset \(S’\) (“input”) and the corresponding model output on \(x\) (“label”). Indeed, obtaining such pairs is rather easy—for a given choice of \(S’\), we retrieve corresponding outputs by just executing the learning algorithm on \(S’\) and evaluating on \(x\).
From this perspective, estimating \(g_\theta\) for a given \(x\) becomes a two-step process:
- Collecting our datamodel train set: Sample a training subset \(S_i\), train a model on \(S_i\), and, finally, add the corresponding “input-label pair” \((S_i, \text{trained model output on }x)\) to our datamodel training set. Rinse and repeat (until that training set becomes sufficiently large).
- Datamodel training: Solve for \(\theta\) by regressing from our “training subsets” \(S_i\) to their corresponding model outputs on \(x\).
Now: how many such input-label pairs do we need to be able to solve the corresponding (very high-dimensional) regression problem? (Note that the dimension here is 50k, the size of the training set!) The answer is: a lot. Specifically, to fit CIFAR-10 datamodels we trained a few hundred thousand CIFAR-10 models. (Moreover, looking across all our paper’s experiments, we train more than 4 million such models in total.) To make this task feasible, we designed (and released!) a fast fast model training library—you might find this library helpful for your training tasks, however big or small. With our library, we were able to bring CIFAR training down to seconds on a single (A100) GPU, meaning that training hundreds of thousands of models takes (only) a few days (on a single machine).
Evaluating datamodels
Now, after all this setup, the key question is: how accurately do such linear datamodels predict model behavior? Following our supervised learning perspective, the gold standard is to evaluate via a held-out test set: a set of (held-out) input-label (or rather, in our case, subset-model output) pairs.
Specifically, we make a datamodel “test set” using the same sampling process employed to generate the datamodel train set. We then compare datamodel-predicted outputs for these (previously unseen) collected subsets to the true outputs (i.e., the output of training a model on the subset and evaluating on the relevant example). It turns out that datamodels predictions predict the result of model training rather well!

The predicted and actual margins here—even conditioned on a specific \(x\)—correspond nearly one-to-one, despite that our predicted margins come from a linear model, and the actual margins stem from thousands of SGD steps on a ResNet-9!
How can we use datamodels?
We’ve already seen that a simple linear model can predict the output of end-to-end model training (for a single target example) relatively well. We found this phenomenon surprising on its own, and hope that studying it further might yield theoretical or empirical insights into the generalization of deep networks (and when applied to new settings, other classes of machine learning models).
That said, in a series of follow up posts we’ll also highlight some of the other direct datamodel applications:
- In Part 2, we’ll take a deeper dive into datamodels’ ability to predict outcomes of model training, and find that this ability extends beyond just the subsets sampled from the distribution they were fitted to. We’ll then use this capability to identify brittle predictions, test examples for which model predictions can be flipped by removing just a small number of examples from the training set.
- In Part 3, we’ll discuss how to use datamodels to identify training examples that are similar to any given test example, and will then employ this capability to find (non-trivial) train-test leakage in both CIFAR-10 and FMoW datasets. (FMoW is the other dataset that we investigate in our paper.)
- In Part 4, we’ll explore leveraging linear datamodels as feature representation. Specifically, we find that datamodels yield a natural way to embed every example into a well-behaved representation space. We use the corresponding embeddings to perform clustering and identify model-driven data subpopulations.
All of these applications are fully detailed in our paper, along with more experiments, a more formal introduction to datamodels, and an extensive discussion of the related and future work in this area. Also, check out our data release with both pre-computed datamodels and predictions corresponding to million CIFAR-10 models. Stay tuned for more!
