Do Large Language Model Benchmarks Test Reliability?

    Paper    Code
Large language models (LLMs) have shown remarkable capabilities in areas like problem-solving, knowledge retrieval, and code generation. Yet, these models still fail sometimes on surprisingly simple tasks. Two such examples that went viral recently were models such as ChatGPT and Claude failing on the questions “how many r’s are in the word strawberry?” and “which is greater, 9.11 or 9.9?”

These examples might seem amusing but inconsequential. However, in safety-critical contexts such as healthcare and finance, simple model errors such as logical or numerical mistakes can have serious ramifications. In fact, mistakes made by LLMs in real-world deployments have already caused legal liability and generated controversy. Given these concerns, it becomes important to understand what kind of tasks LLMs can perform reliably—that is, tasks that these models can consistently perform correctly.

So, how can we identify what kinds of tasks LLMs are actually reliable on?

“Saturated” Benchmarks

A good place to start our investigation is by looking at older, existing benchmarks. These benchmarks tend to evaluate simpler tasks; tasks that are easy enough that one might expect today’s LLMs to be reliable on them.

An example of such a benchmark is GSM8K, which consists of grade-school math problems. When GSM8K was first released, models achieved less than 40% on it, but today, our best LLMs achieve over 95%! In the last year, however, progress on this benchmark has stalled, and concerns have been raised by the community over the label noise, e.g., mislabeled or poorly written questions, in GSM8K, such as illustrated in the following tweet:

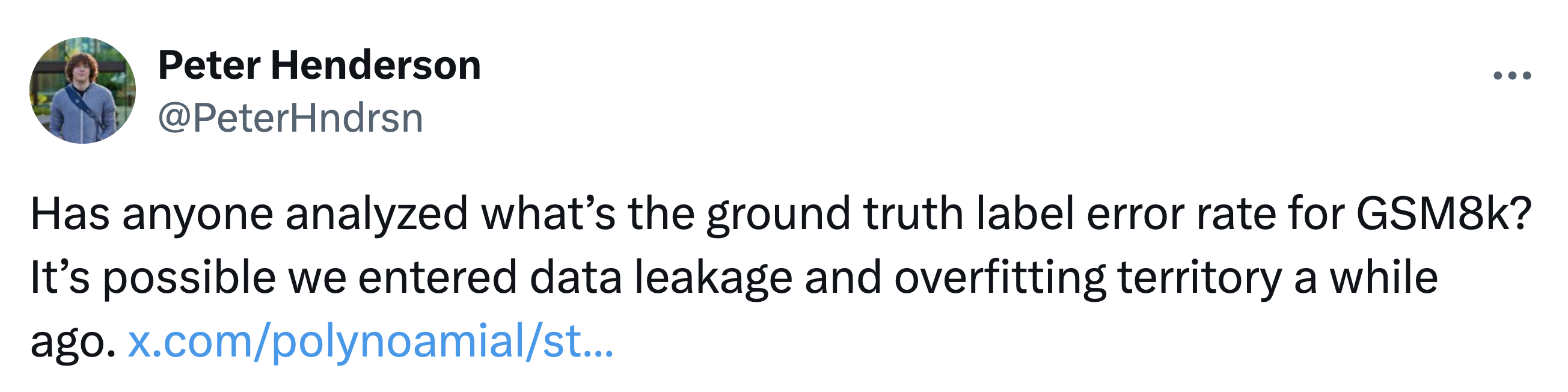
In fact, recent releases of models including OpenAI o1 and the new Claude 3.5 Sonnet have excluded evaluations on GSM8K, opting instead to evaluate on more challenging benchmarks.

GSM8K is just one of many benchmarks that have met this fate. Specifically, LLMs have improved so much on many older benchmarks that the community views them as “saturated”, i.e., that models have reached sufficient (or even human-level) performance on them, and there isn’t any room left for improvement. Like GSM8K, such benchmarks are typically discarded in favor of newer, harder ones.

It is important to note, however, that benchmarks are often considered to be saturated even before models actually reach 100% accuracy on them (recall that GSM8K accuracy has plateaued at around 95%). The lingering models’ errors are typically dismissed as label noise within the benchmark itself.

If we really care about reliability, though, we might not be satisfied with “graduating” saturated benchmarks like GSM8K until we better understand what’s causing those 5% remaining errors. Maybe all of these remaining errors can be attributed to label noise, as the tweet is hinting at, and our current models have already reached truly reliable performance. Or maybe, might there be genuine model errors/failure modes lingering within the 5%, hidden among the label noise?

In other words, we might be declaring benchmarks as saturated too early, leading us to overlook fundamental reliability gaps in our models.

Towards Platinum Benchmarks

To figure out what’s really going on, we looked through the questions within fifteen such benchmarks to identify and remove any mislabeled or poorly written questions within them.

Unfortunately, manually inspecting every example from a benchmark would be extremely time-consuming (or, to be precise, student-time-consuming). Therefore, to speed up the process, we first show each question to many different LLMs, and then inspect any question where at least one model made a mistake. Here are examples of questions that this procedure yielded (and that turned out to be genuine label errors):

We use this process to clean all fifteen benchmarks, and it turns out that many “saturated” benchmarks are indeed riddled with issues! Below, we show the average number of errors that LLMs make on each benchmark before and after we clean them. This can tell us what percent of model errors on the original benchmark can be attributed to issues with the benchmarks themselves.

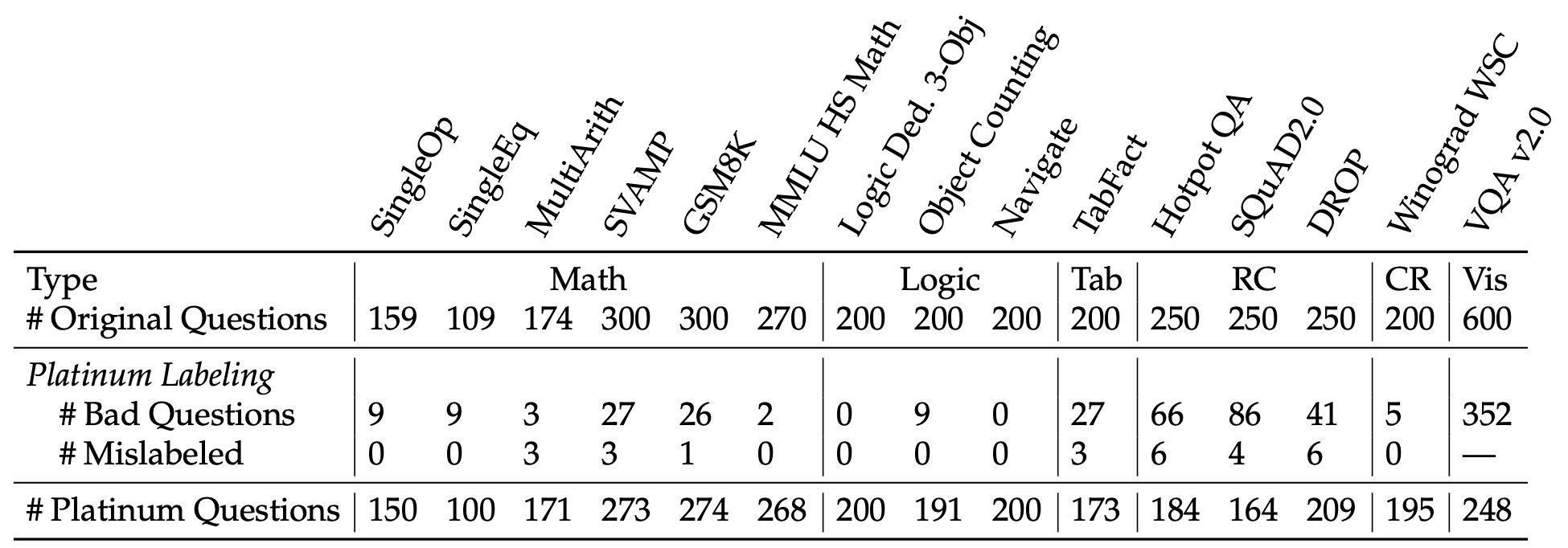
In fact, we find that on more than half of the original benchmarks, any reported model error is more likely to be caused by issues with the benchmark rather than the model!

Now that we have cleaned up these benchmarks, what can they tell us about LLM reliability?

Platinum benchmarks reveal significant reliability gaps

Turns out today’s LLMs might not be as reliable as one might hope! Below we display the number of errors our models make on each of these fifteen benchmarks. We are also releasing a public leaderboard that we’ll continue to update as we add new models and further revise these benchmarks.

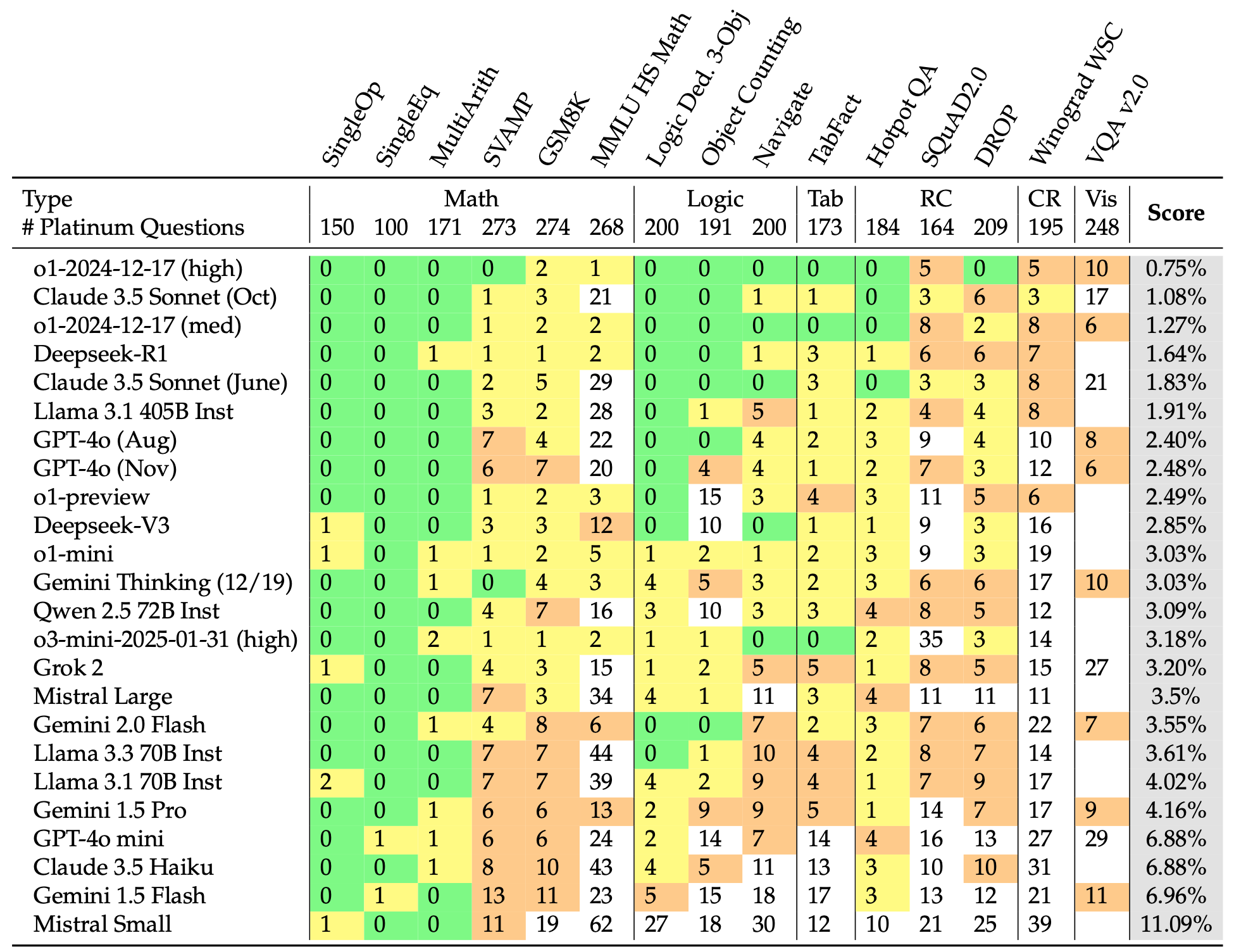
As we can observe, current frontier models actually still make many genuine errors on these “saturated” benchmarks, which is worrying if we care about their reliability; even though current models can solve PhD-level questions (e.g., GPQA), they continue to make simple mistakes on elementary-school level tasks.

Yet, as we saw previously, current benchmarks are too noisy to properly quantify this kind of reliability, making it impossible to tell when models might actually be ready for deployment. These findings highlight the need to rethink how we construct benchmarks so that they provide us with an accurate grasp of the models’ unreliable behavior (if any). In particular, we need better ways to leverage tools such as LLMs in this process, so as to (dependably) reduce our reliance on manual inspection and annotation.

Using platinum benchmarks to discover patterns of failures

So far, our platinum benchmarks have given us a broader view of LLM reliability, suggesting that these models make mistakes on surprisingly simple tasks. But what do these failures actually look like? Are they random, or indicative of a pattern?

While we were looking through some simple math world problems included in our platinum benchmarks, we noticed the following problem that Claude 3.5 Sonnet gets wrong:

This seems like a pretty simple problem, so what happened here? Let’s take a look at how Claude got to its (incorrect) solution:

It turns out that Claude decided to round up the answer to get to a whole number, even though the division already resulted in a whole number. Looking through more math problems, we actually find a second time that Claude makes this same mistake!

In both of these problems, the last step is a division that ends in a whole number, and Claude rounds up the answer even though it shouldn’t. We also noticed that in both cases, the true solution is either prime or close to prime (737 is the product of two prime numbers). Is this just a coincidence?

To find out, let’s rerun Claude on more problems like these, but vary the numbers to change how “prime” the answer is. Specifically, we construct templates for more word problems similar to the ones above, like the following:

Let’s see how often the model fails as we vary how “prime” n is:

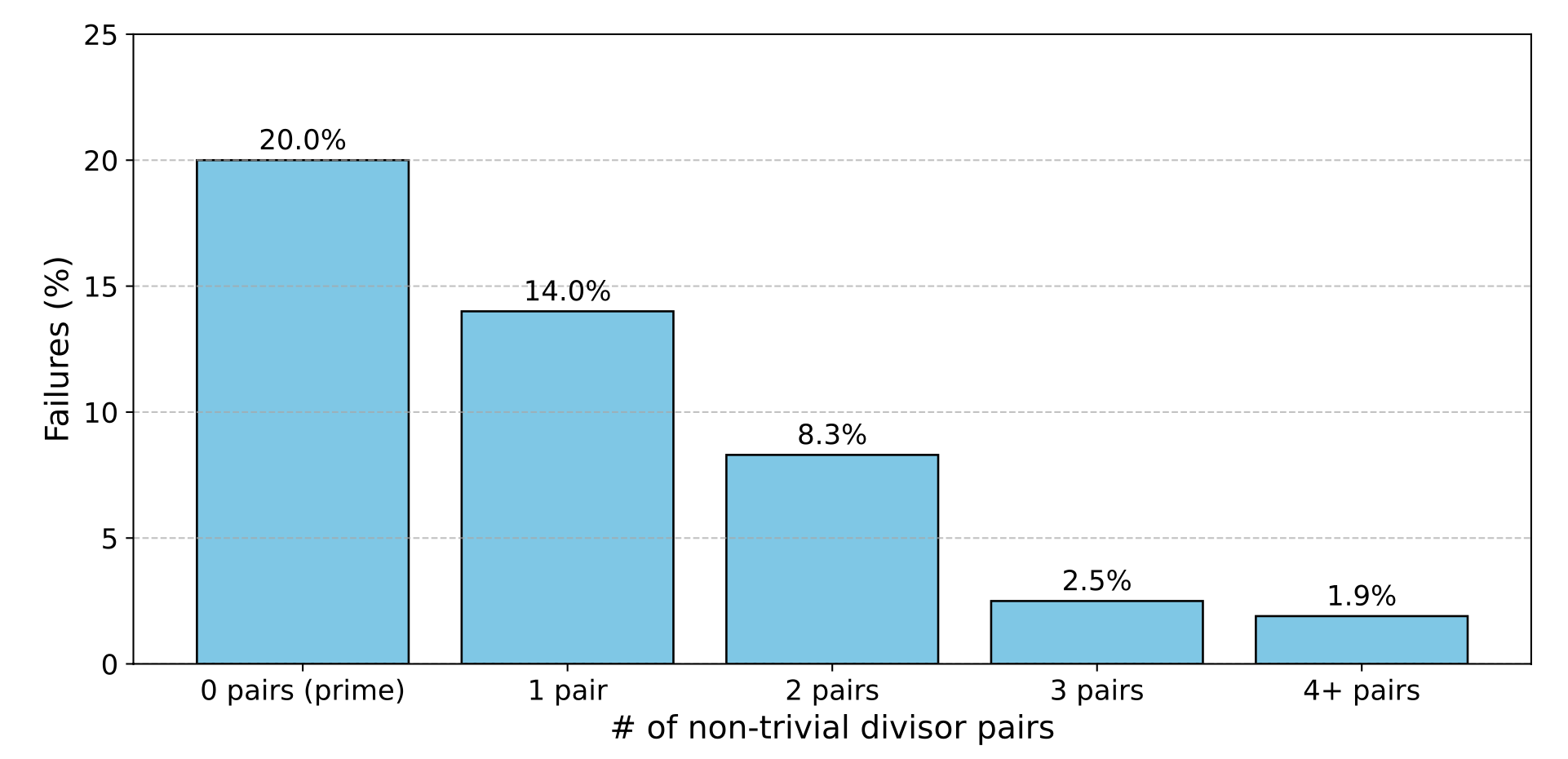
We find that, indeed, this failure is closely related to how close to prime the answer is. How strange! Where could this kind of consistent failure come from?

Summary

In this post, we took a step back and revisited some of the most popular natural language model benchmarks, many of which the community has deemed to be “saturated.” We found that many of these benchmarks might have been discarded as “solved” too early, as today’s LLMs still continue to exhibit genuine failures on them, highlighting a widespread lack of reliability.

To remedy this gap in our benchmarking practices, we proposed the construction of platinum benchmarks and showed how they can better evaluate reliability. We hope our work will be a first step in a more rigorous practice of quantifying such reliability.