Pre-training on a large and diverse dataset and then fine-tuning on a task-specific dataset is a popular strategy for developing models that are robust to distribution shifts. In our most recent work, we develop a more fine-grained understanding of this approach, identifying specific failure modes that pre-training can and cannot address.
Suppose that we would like to develop a model that distinguishes between cats and dogs. We collect photos of each type of animal and train a model on this dataset. When we deploy our model, though, it might encounter photos of cats and dogs that look different—for example, the animals might appear on different backgrounds or the photos might be taken with a different camera. Such distribution shifts between the data used to develop a model (the “reference” distribution) and the data it actually encounters (the “shifted” distribution) often cause models to underperform. How, then, can we develop a model that we can deploy confidently?
One potential solution is to expose our model to more (and, in particular, more diverse) data. Finding additional task-specific data might be difficult though. Can we instead pre-train a model on a large and diverse general-purpose dataset (e.g., ImageNet, JFT-300M, LAION-5B) and then fine-tune it on the (small amount of) task-specific data that we’ve collected?
Indeed, such pre-trained and fine-tuned models turn out to be substantially more reliable under distribution shifts than models trained “from scratch” on a task-specific dataset. Yet, sometimes pre-training does not help at all, even with a very large and diverse pre-training dataset. In our latest paper, we ask: why does pre-training help significantly under some distribution shifts but not at all under others? In particular, as models and pre-training datasets grow, will there remain failures that pre-training cannot address?
Background: measuring robustness
Let’s start by defining what it actually means for pre-training to “help.” We might initially consider just measuring performance on the shifted distribution to quantify how robust a model is. However, this performance might depend on choices which have nothing to do with whether a model is pre-trained (e.g., architecture, hyperparameters). To measure the robustness gains that stem specifically from pre-training, we would like a way to measure robustness that is agnostic to these choices. It turns out that different models trained from scratch (with different architectures, hyperparameters, etc.) often exhibit a strong linear relationship between their accuracies on the reference and shifted distributions.
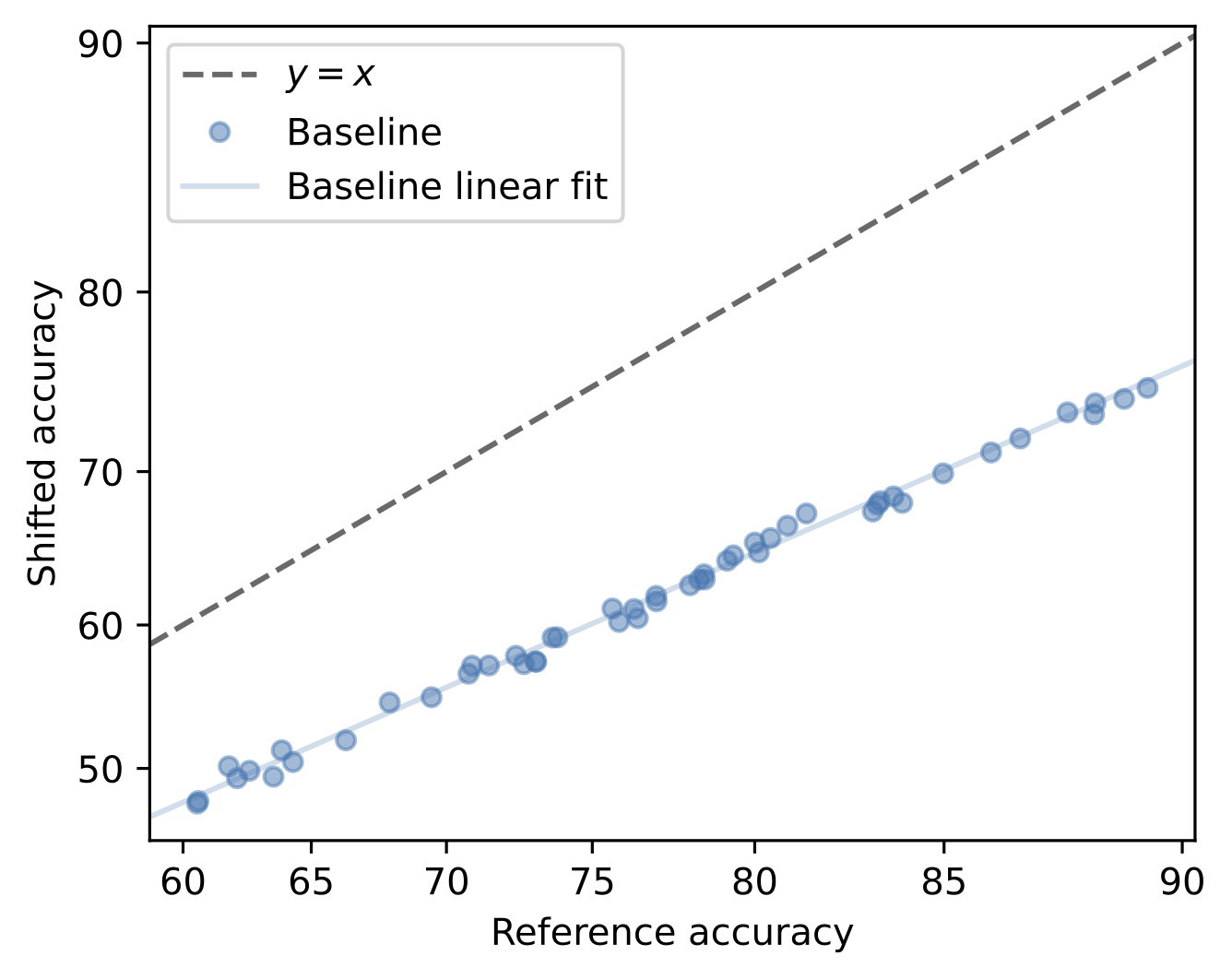
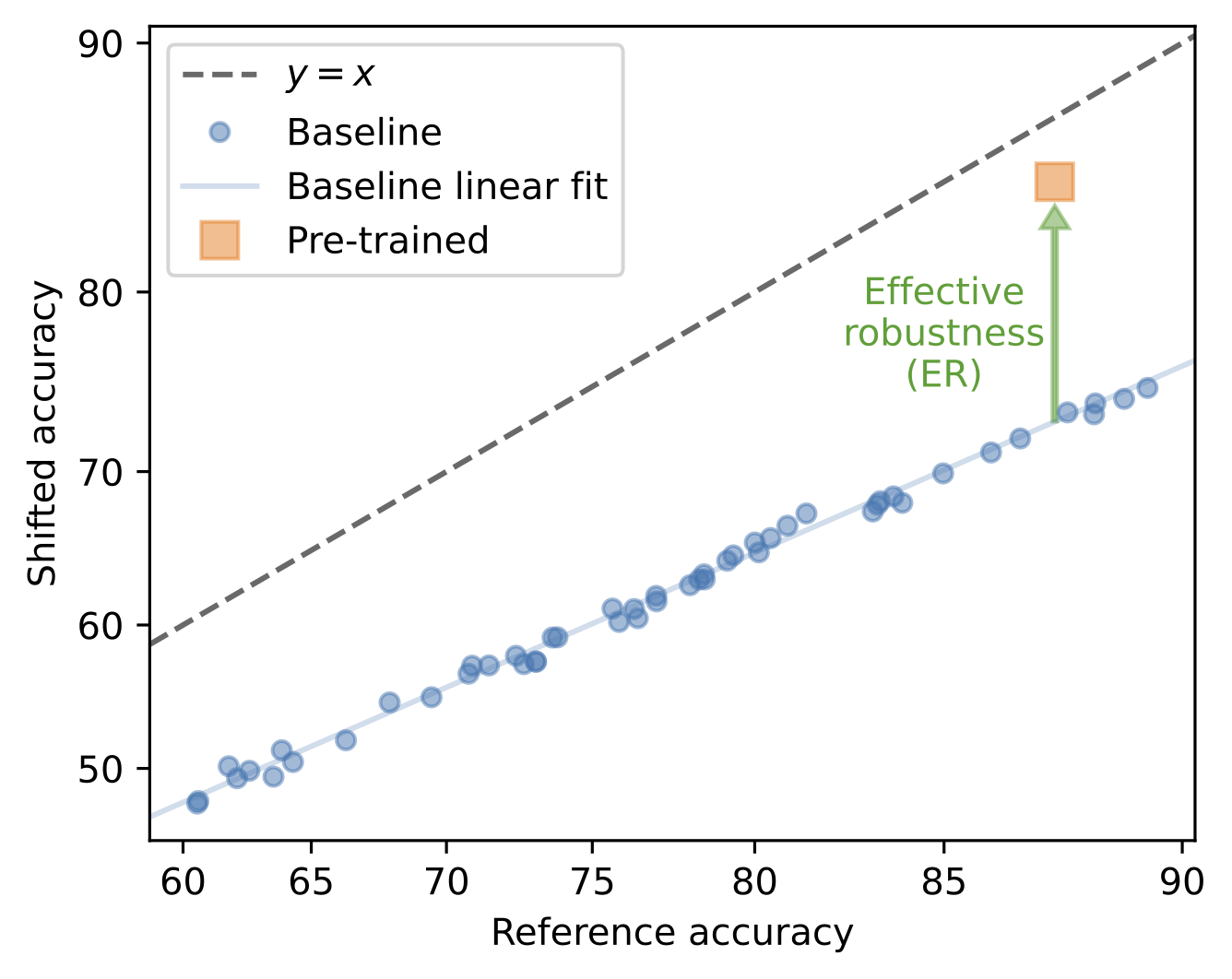
In a sense, models trained from scratch are often similarly robust despite their performances varying. So, we can quantify the robustness benefits of pre-training by measuring how much a pre-trained model improves over this trend—a metric known as effective robustness (ER).
Let’s now measure the effective robustness of a variety of pre-trained models on two distribution shifts of ImageNet: ImageNet-V2 and ImageNet Sketch.
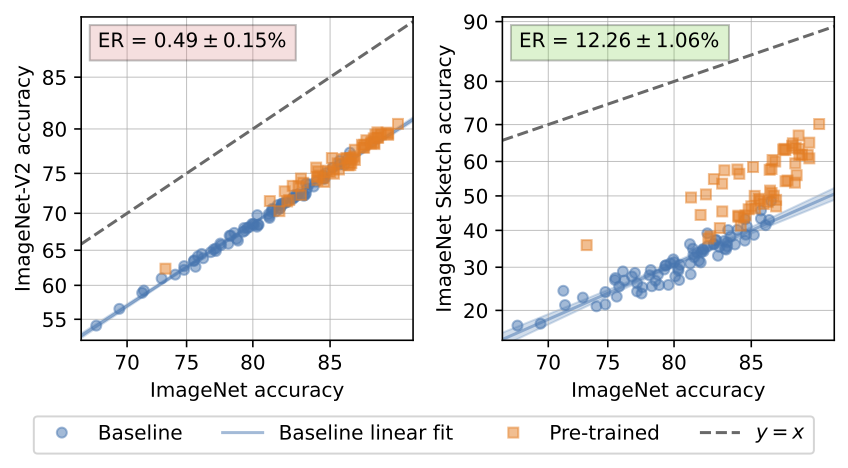
While some pre-trained models exhibit substantial effective robustness to ImageNet Sketch, the highest effective robustness attained by any of these models on ImageNet-V2 is just 1.80%. The issue here doesn’t seem to be the scale or quality of the pre-trained models—the largest of these models has 1B parameters and is trained on a diverse dataset of 2B image-text pairs. This observation motivates our central question: are there certain types of failures that pre-training alone cannot address?
Why do models fail under distribution shift?
To answer this question, let’s first consider why a model might fail under distribution shift.
Suppose that the photos of cats and dogs that we collected were all taken during the day. A model that we train on this data might then be sensitive to lighting conditions. After all, to perform well on its reference distribution the model would only need to correctly classify photos with daytime lighting. As a result, the model might fail if it encounters photos taken at night when deployed. In other words, the model may extrapolate poorly outside of the reference distribution.
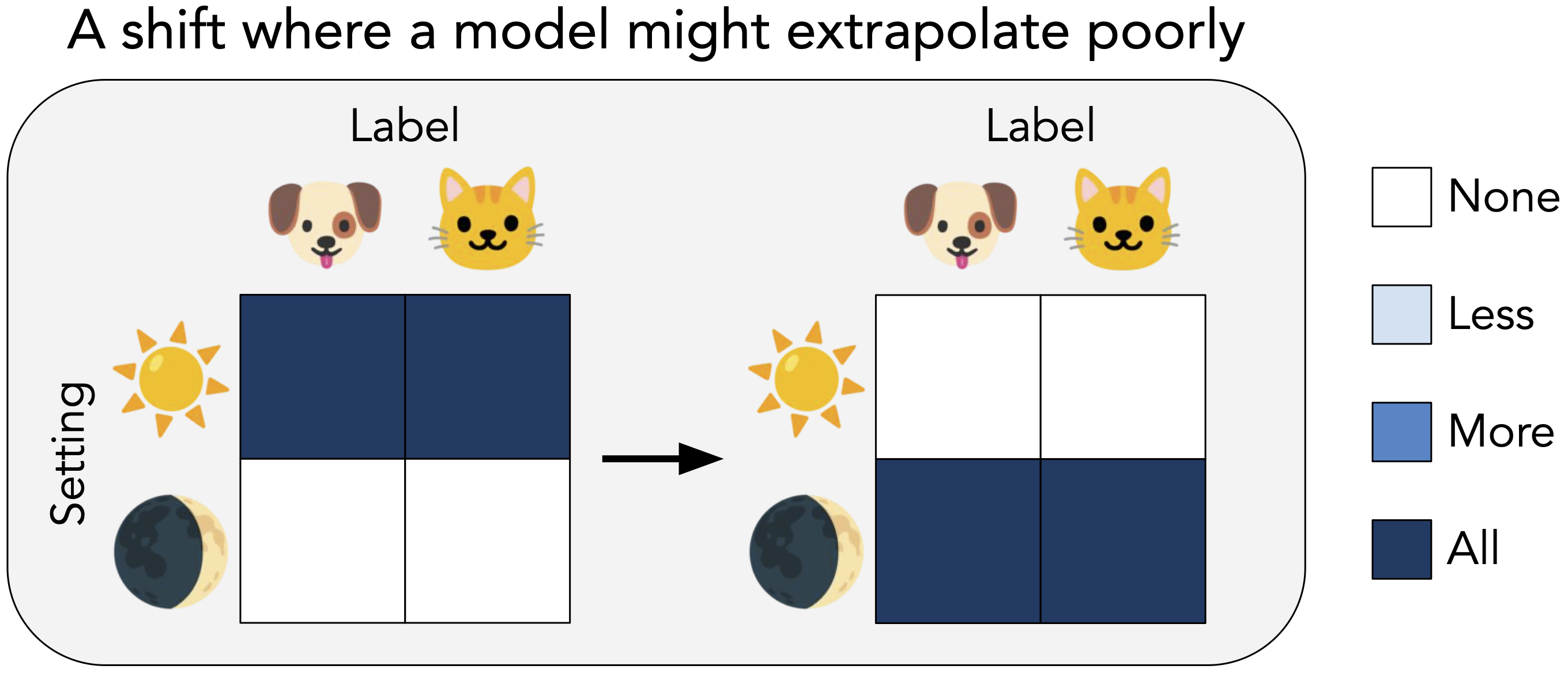
A model can also underperform even when it does not encounter anything “new.” Suppose that when we collect photos of cats and dogs, the majority of cats appear indoors while the majority of dogs appear outdoors. In other words, the setting is spuriously correlated with the animal. A model that we train on this data would likely rely (at least in part) on the background (see our previous post), despite it being intended to classify cats vs. dogs. Thus, if a model encounters more photos of cats outdoors and dogs indoors when deployed, its performance would drop. In this case, the model would fail because it picks up a harmful bias from the reference distribution.
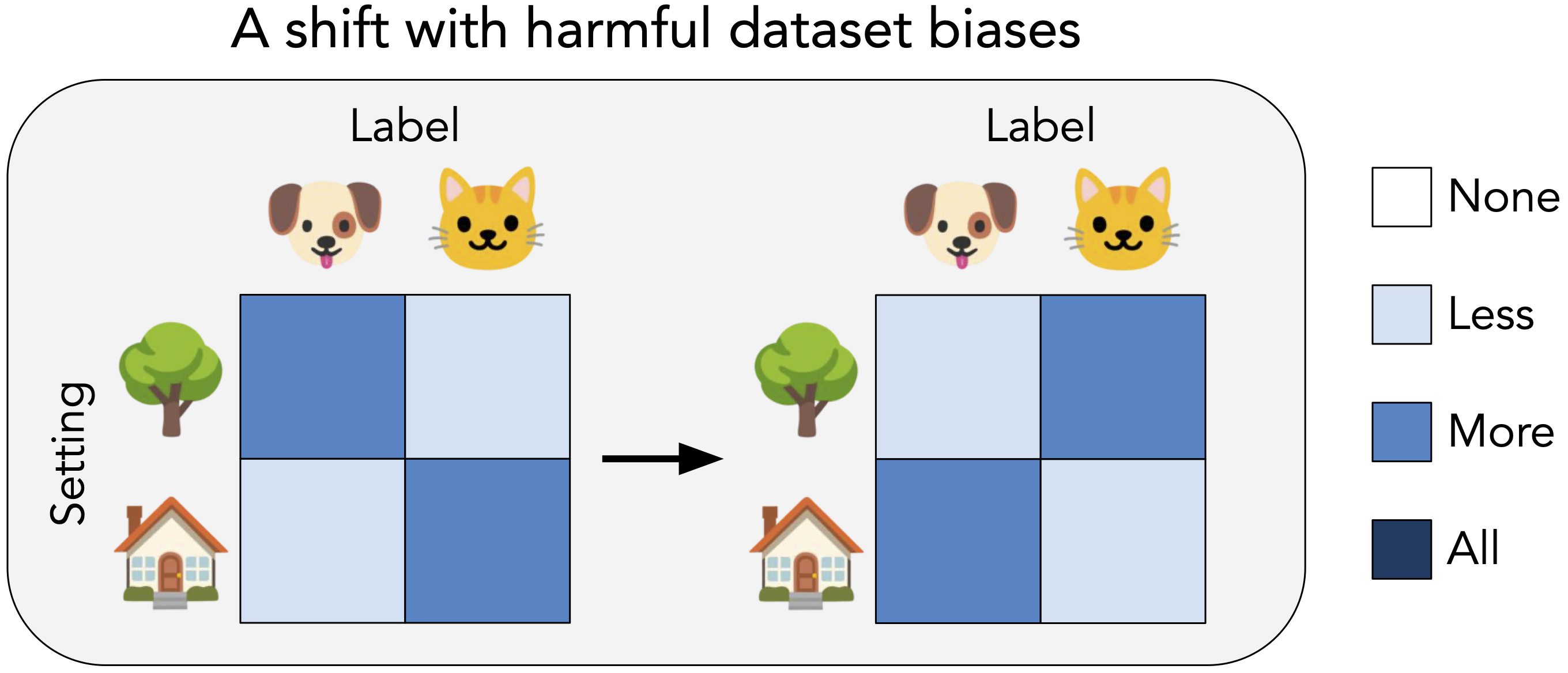
When can pre-training help?
Which of these failure modes can pre-training address? To build intuition, in our paper we first study a simple logistic regression setting. Our findings suggest the following rule of thumb: pre-training helps specifically with extrapolation and cannot address harmful dataset biases!
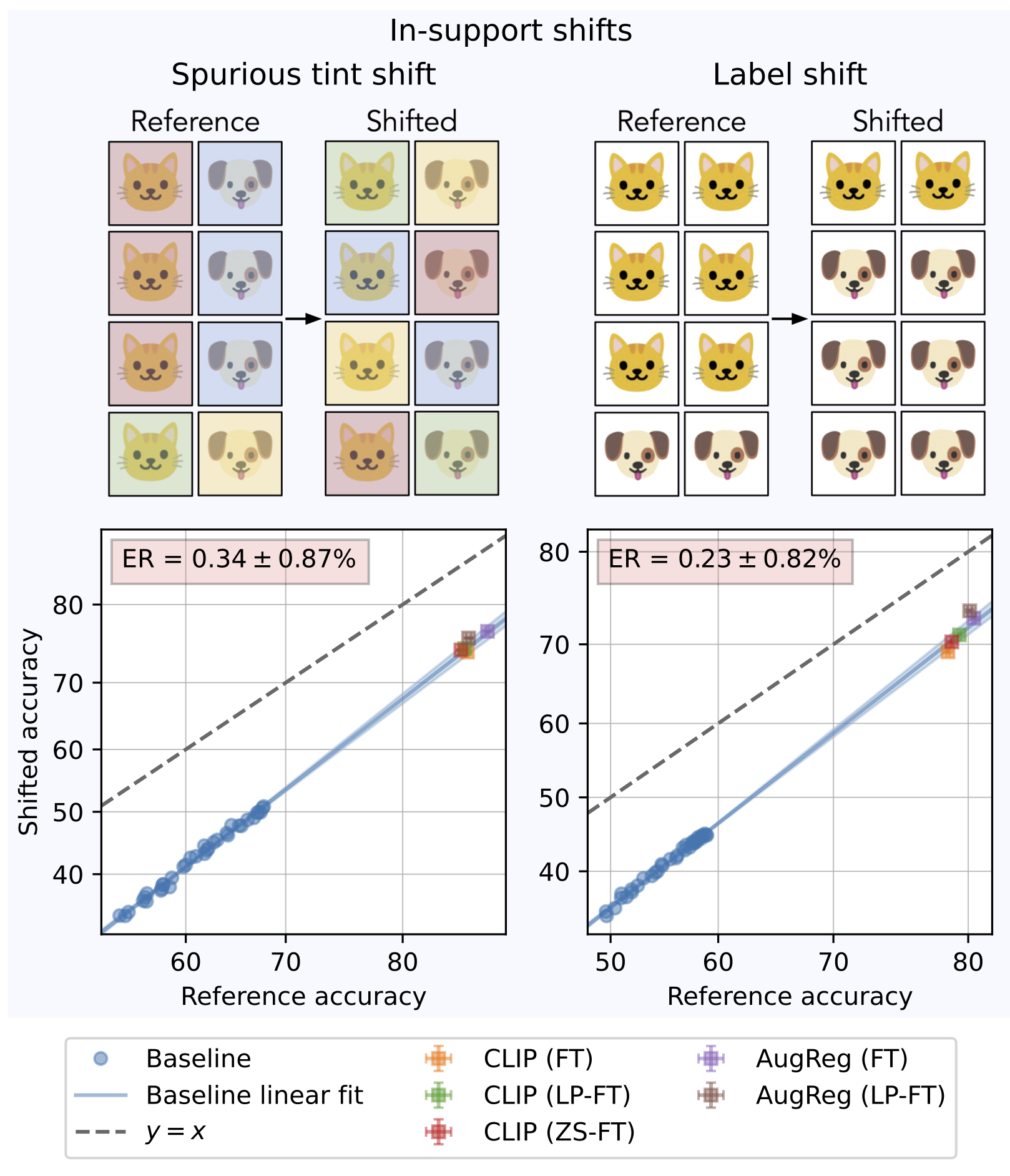
Isolating the two failure modes: in-support and out-of-support shifts
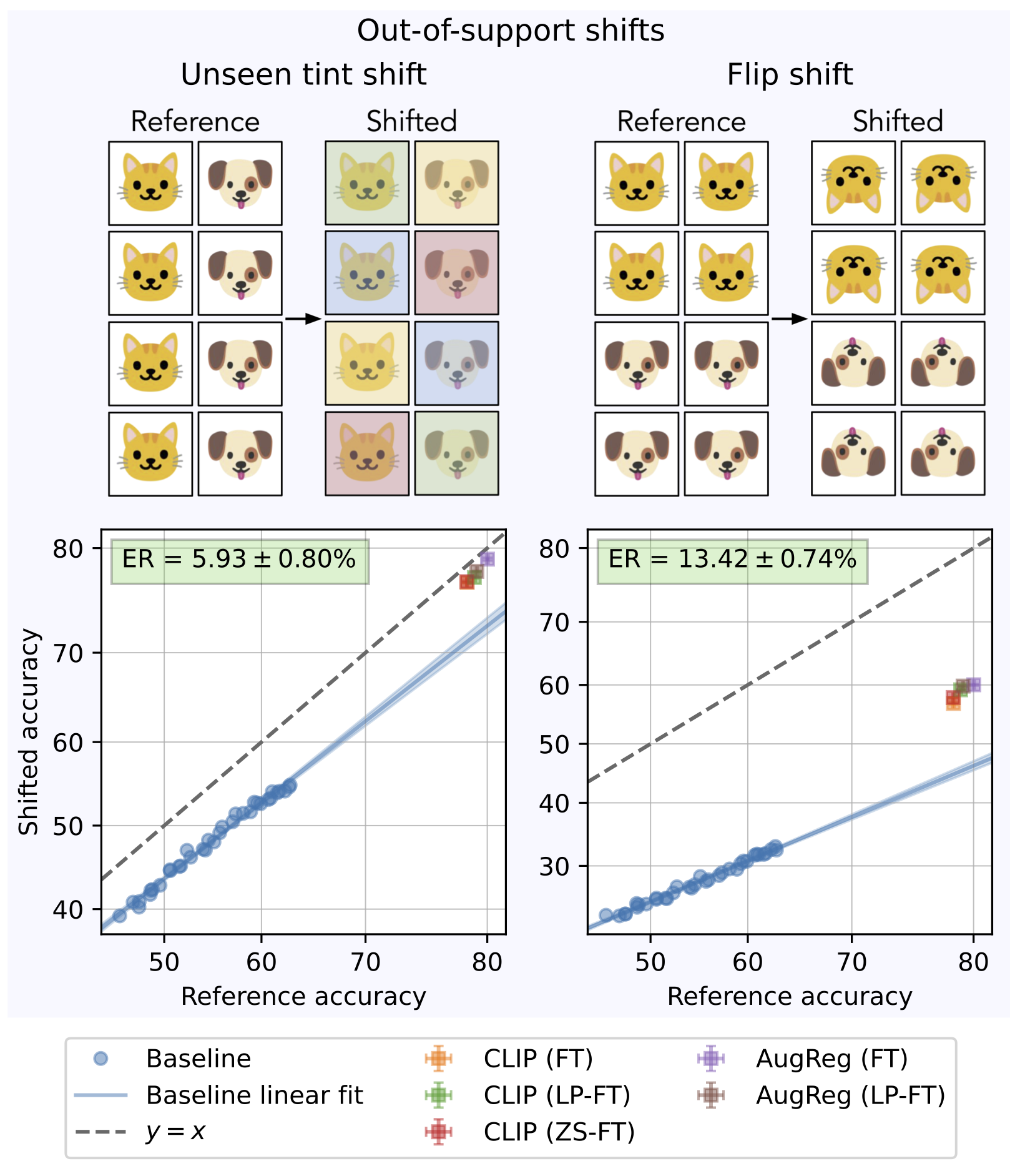
To examine this hypothesis, we’ll need a way to isolate the two types of failures. We do so by defining two categories of distribution shift. First, if the shifted distribution does not include anything “new,” then a model cannot fail because it extrapolates poorly but might fail due to dataset biases. We refer to such shifts as in-support. Second, if the shifted distribution contains examples outside of the reference distribution, then a model can underperform for any reason. We call these shifts out-of-support. So, if pre-training specifically improves extrapolation, it should be able to help on out-of-support shifts but not in-support shifts.
Constructing synthetic in-support and out-of-support shifts
Let’s now measure the robustness that pre-training provides on in-support and out-of-support shifts. To start, we construct a few synthetic shifts of each type by modifying ImageNet. For example, we create a “spurious tint shift” by adding a tint to the original ImageNet examples that is spuriously correlated with the label in the reference dataset but not the shifted dataset. We find that, as suggested by our rule of thumb, pre-training provides minimal effective robustness to in-support shifts.
Meanwhile, pre-training can substantially improve robustness to out-of-support shifts.
Dividing natural shifts into in-support and out-of-support splits
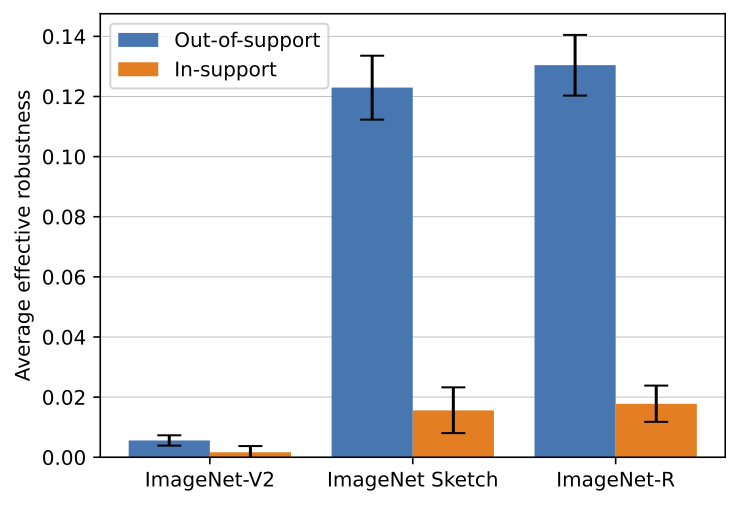
Does this finding hold more broadly, and, in particular, on natural distribution shifts? It’s hard to find natural distribution shifts that are “purely” in-support, so we instead divide natural shifts into an “in-support split” and an “out-of-support split” (we leave the details to our paper). For example, for a distribution shift from ImageNet to ImageNet Sketch (a dataset consisting of sketches of ImageNet classes), the in-support split contains examples that look more photorealistic while the out-of-support split contains examples that are more clearly sketches:

We split three natural distribution shifts of ImageNet in this way. We once again find that pre-training can provide significant robustness gains on out-of-support examples but not on in-support examples.
Conclusion
In this post, we study the robustness of pre-trained and fine-tuned models to specific types of failures. We find that, as a rule of thumb, pre-training can help with extrapolation but cannot address harmful dataset biases. In light of this finding, dataset biases present a fundamental limitation that cannot be overcome by simply leveraging additional pre-training data or larger models. We thus encourage practitioners not to treat pre-training as a panacea for robustness. Instead, they should consider the specific failure modes they might encounter, i.e., “ask their distribution shift,” to determine if pre-training can help. Guided by this understanding, in a follow up post, we’ll investigate how we can effectively harness pre-training to develop robust models.
