In our latest paper, we provide a new perspective on data poisoning (backdoor) attacks. We show that without assumptions on the attack, backdoor triggers are indistinguishable from features already present in the dataset. In our work, we assume that backdoors correspond to the strongest feature present in the data, and we leverage datamodels to detect backdoored inputs.
Backdoor Attacks
Consider a scenario in which an adversary wants to use their power to modify a small subset of a machine learning model’s training inputs to introduce a test-time vulnerability. One example approach to accomplishing could involve the adversary adding a small red square to some images of the training set, and then re-labeling them as “plane:”

Then, at test time, the adversary is able to fool the model into classifying anything as a plane just by adding the same red square!

The red square in the above example is what we typically call a “trigger,” “backdoor,” or “backdoor pattern,” and the end-to-end procedure is called a “backdoor attack.” Because the adversary only needs to modify a tiny fraction of the training set to launch an attack, backdoor attacks can be extremely difficult to detect or defend against.
Backdoor attacks: A different perspective
The prevailing approach to defending against backdoor attacks treats these manipulated images as anomalies/outliers in the data (and then tries to remove them). This approach is quite natural, as it allows us to draw from a long line of work in robust statistics on data poisoning.
In a typical data poisoning setup, one receives data where $(1 - \varepsilon)$-fraction is sampled from a known distribution $D$ and the remaining $\varepsilon$-fraction is chosen by an adversary. The goal is then to detect the adversarially chosen inputs, or to learn a good classifier in spite of the presence of these inputs. This perspective has led to a line of defenses against backdoor attacks. But is it the right way to approach the problem?
In particular, in the classical data poisoning setting, leveraging the structure of the distribution $D$ is essential to obtaining any (theoretical) guarantees. However, in settings such as computer vision, it is unclear whether such structure is available. In fact, we lack almost any formal characterization of how image datasets are distributed.
In fact, as we can show, without strong assumptions on the structure of the input data, backdoor triggers are indistinguishable from features already present in the dataset. Indeed, let us illustrate this point with two experiments.
Backdoors can look like plausible features
Imagine we train a model on a version of ImageNet where we added hats to some of the cats:

It turns out that the resulting model is very sensitive to the presence of hats—making it effectively a backdoor trigger. That is, at inference time, the model most commonly predicts “cat” when provided images with hats:
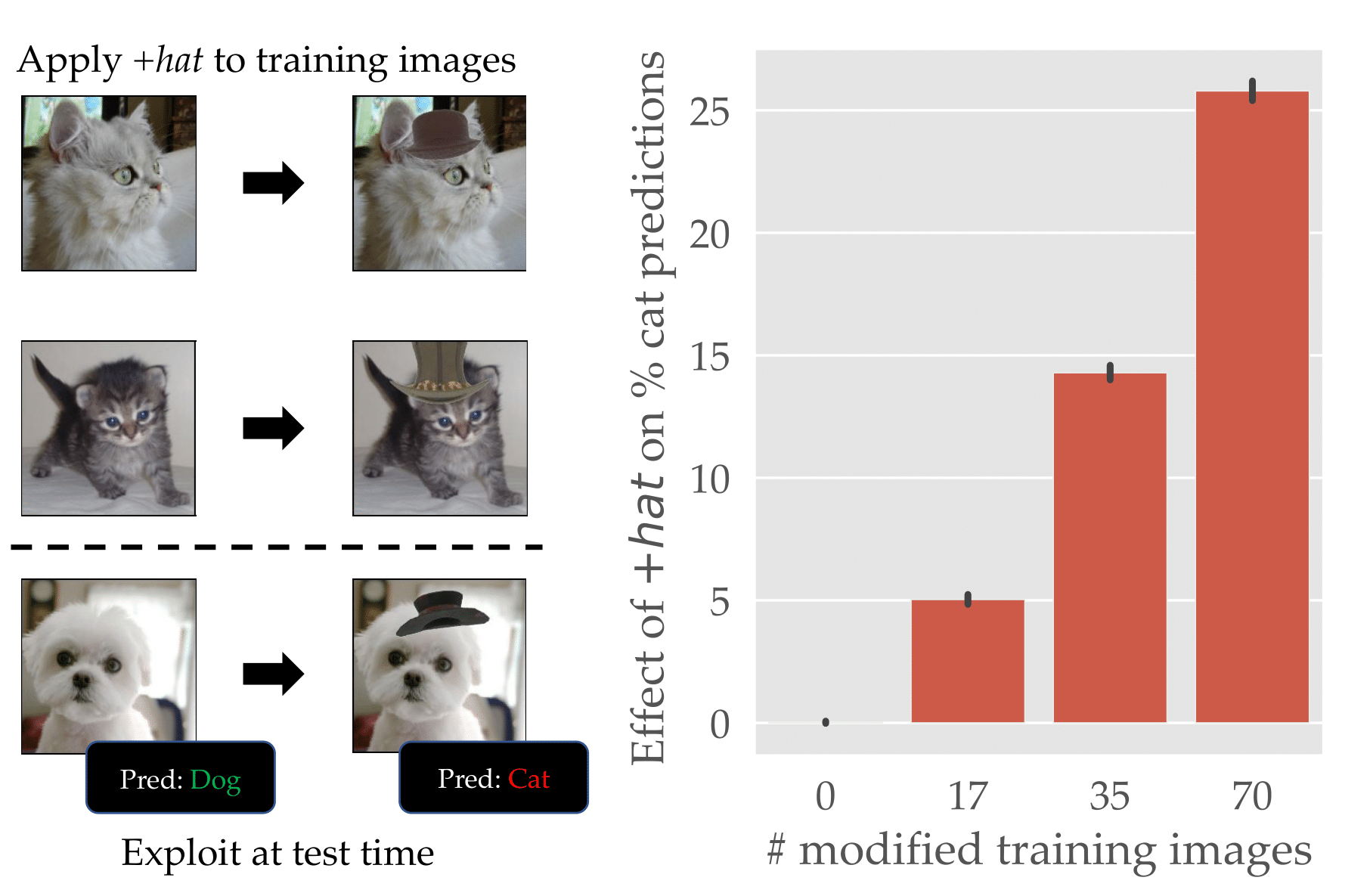
Is this a backdoor attack? On one hand, we did in fact add a “trigger” to a subset of images that allowed us to manipulate test-time predictions. On the other hand, however, the dataset still contains only “natural images”—there’s nothing specific about our hat trigger that makes it different from any other feature like “fur” or “whiskers.”
Backdoors can occur naturally
In fact, we can even avoid the need to add any new features, and just leverage the features that already are present in the data. For example, ImageNet has a “tennis ball” class that consists largely of images that have a “small yellow ball” in them:

What happens if we superimpose a small yellow circle on images from other classes at inference time? It turns out that the small yellow ball serves as a reliable trigger!
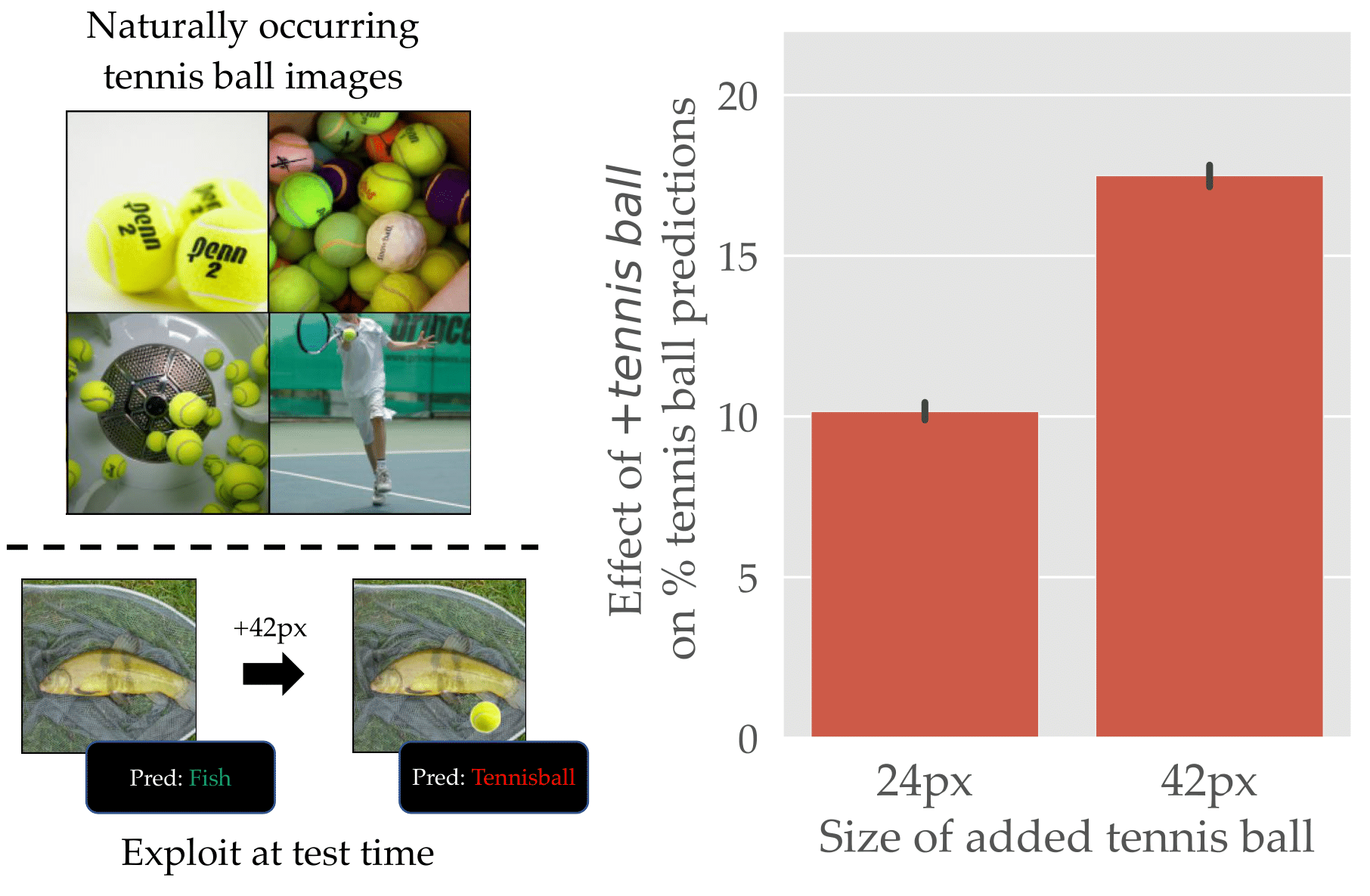
Now, is this a backdoor attack? On one hand, by overlaying a simple pattern at inference time we were able to easily manipulate the predictions, just like the adversary was in our red square example above. On the other hand, no adversary has manipulated the dataset!
The key conclusion from the above two experiments is that without any assumption about the nature of the attack, an adversary can leverage any feature present in the dataset to execute a successful backdoor attack. As a result, the only way to distinguish a backdoor attack from a naturally-occurring feature is by making some kind of assumption on the structure of the data or of the backdoor attack.
In our paper, we further corroborate this conclusion by showing how all prior backdoor defenses make (often implicit) assumptions about the structure of backdoor attack—for example, they might assume that the backdoor attack has a certain visual structure, or that backdoor images are separated from natural data in the latent space of a pre-trained network.
An alternative assumption
Ok, so we clearly need to make an assumption to even properly define what a backdoor attack is. What is the “right” assumption to make though? In our work, we propose a new assumption, one that is independent of how the trigger looks, but rather a one that is directly related to how the backdoor attack behaves. In particular, we choose to make assumptions about the effect backdoor triggers have on model predictions. That is, we assume that the backdoor feature corresponds to the strongest feature present in the dataset. (Note that this assumption is tied to the success of the backdoor attack itself. If the backdoor trigger was not the strongest feature, then there exists another feature that could be used as a more effective backdoor, and that feature should be the one detected by backdoor defenses.)
In our paper, we provide a formal definition of that assumption and, in particular, of what “strength” means but, intuitively, for a feature $\phi$, we measure the strength of that feature by measuring how much adding one example with feature $\phi$ to the training set helps models classify other examples with feature $\phi$.
The resulting approach to backdoor defense
Now that we have a notion of “feature strength”, we show in our paper that we
can leverage datamodels,
The resulting algorithm is as follows:
- For a task with training set $S$, a datamodel for an example $x$ is a vector $\theta \in \mathbb{R}^{|S|}$ that has one entry per training example, measuring how important each training example is to correctly classifying $x$.
- We compute datamodels for each point in the training set: the result is an $|S| \times |S|$ matrix where each row is a datamodel for training example $(x_i, y_i)$.
- We show that our assumption implies that if $x_i$ has the backdoor feature, it must have significant dependence on other examples with the backdoor feature, and so the corresponding entries in its datamodel vector must be especially large.
- This in turn means that in the $|S| \times |S|$ datamodel matrix, the backdoor examples make up an especially large submatrix–—in fact, we show that our assumption implies that the backdoor examples are the maximum-sum submatrix of the datamodel matrix.
- Since finding the maximum-sum submatrix of a given size is a difficult problem, we use heuristics to approximate each row’s likelihood of being a part of the maximum-sum submatrix, which we then use as a risk score telling us whether to remove the corresponding example.
Experiments and Results
In our paper, we demonstrate the effectiveness of our algorithm against a suite of standard backdoor attacks. We compare to a variety of baselines and show that our primitive successfully identifies the backdoor examples, often without any tuning.
Conclusion
In this blogpost, we presented a new perspective on data poisoning. Specifically, we argued that backdoor triggers are fundamentally indistinguishable from existing features in the data. As a consequence, we argued that we need assumptions to be able to distinguish these triggers from other features present in the dataset. We then proposed to make an assumption that backdoor triggers are features with a particularly strong effect on a model’s predictions. Equipped with this perspective (and assumption), we designed a primitive for detecting training input containing backdoor tiggers. Through a wide range of experiments, we demonstrated the effectiveness of our approach in defending against backdoor attacks, while retaining high accuracy.
