Read the paper Download the notebooks
This post discusses our latest paper on deep network representations—while representations of standard networks are brittle and thus not fully reflective of the input geometry, we find that the representations of robust networks are amenable to all sorts of manipulation, and can truly be thought of (and dealt with) as just high-level feature representations. Our work suggests that robustness might be more broadly useful than just protection against adversarial examples.
One of the most promising aspects of deep neural networks is their potential to learn high-level features that are useful beyond the classification task at hand. Our mental model of deep learning classifiers is often similar to the following diagram, in which the networks learns progressively higher-level features until the final layer, which acts as a linear classifier over these high-level features:
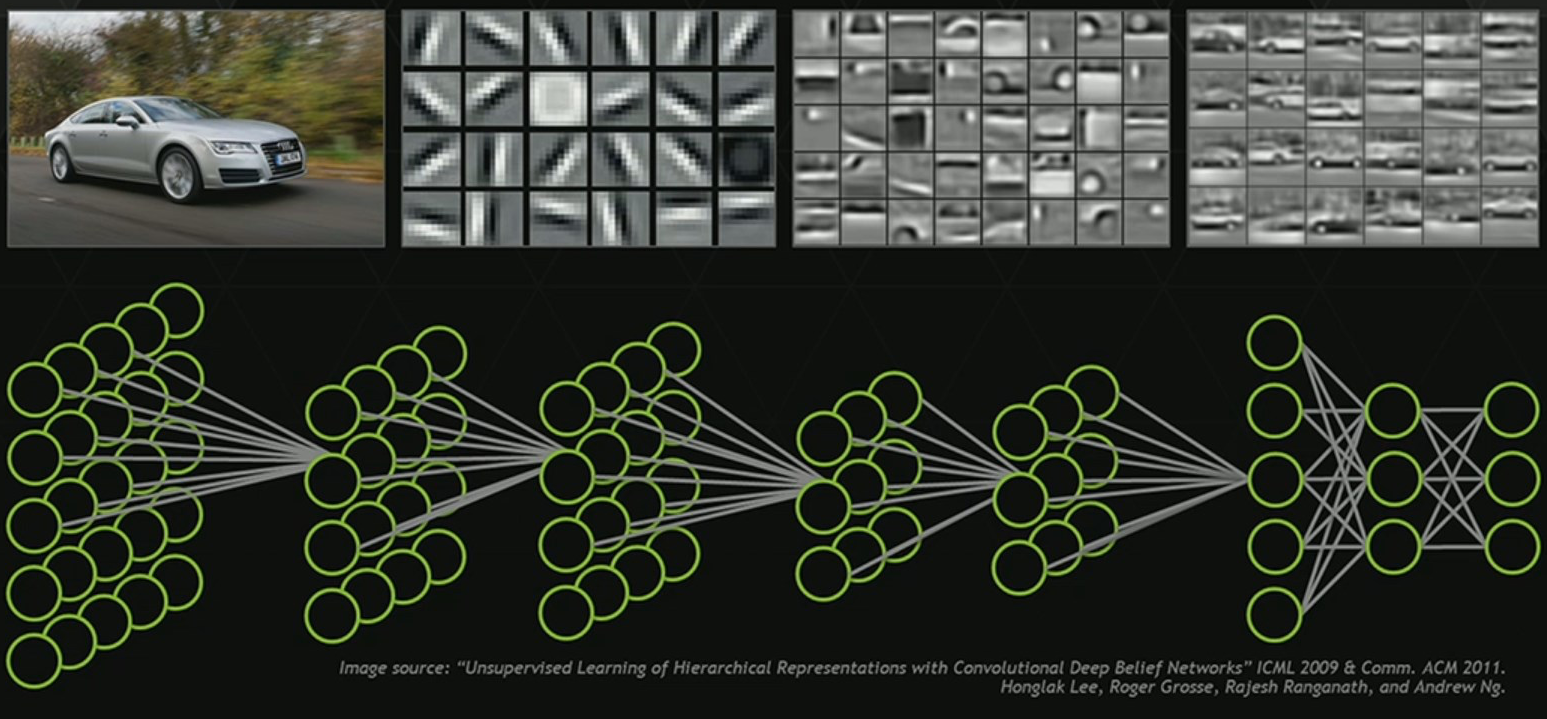
This picture is consistent with the surprising versatility of deep neural network feature representations—learned representations for one task are useful for many others (as in transfer learning), and distance in representation space has often been proposed as a perceptual metric on natural images (as in VGG distance).
But to what extent is this picture accurate? It turns out that it is rather simple to (consistently) construct images that are completely different to a human, but share very similar representations:
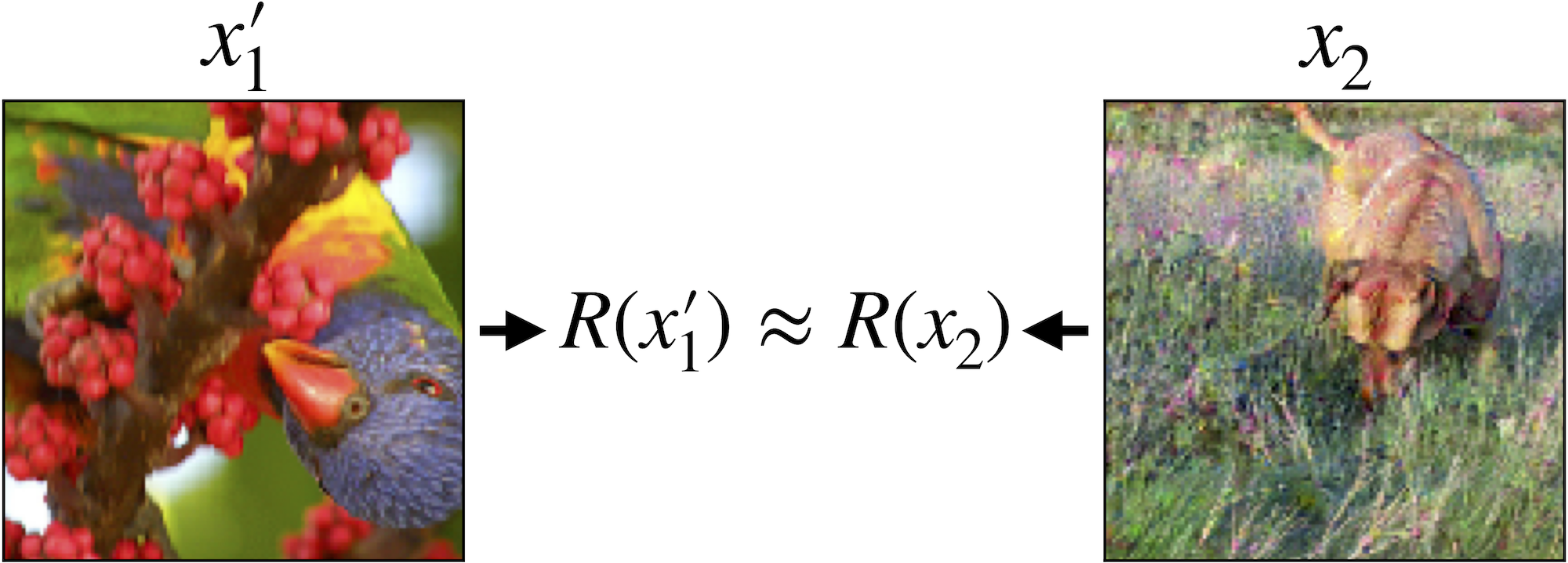
This phenomenon is somewhat troubling for our conceptual picture: if feature representations actually encode high-level, human-meaningful features, we should not be able to find two images with totally different features that the model “sees” as very similar.
The phenomenon at play here turns out to be more fundamental than just pairs of images with similar representations. Indeed, the representations of neural networks seem to be pervasively brittle: they can be manipulated arbitrarily without meaningful change to the input. (In fact, this brittleness is similar to the phenomenon that we exploit when making adversarial examples.)
Clearly, this brittleness precludes standard representations from acting how we want them to—in particular, distance in representation space is not fully aligned with our human perception of distance in feature space. So, how might we go about fixing this issue?
Adversarial Robustness as a Feature Prior
Unfortunately, we don’t have a way to explicitly control which features models learn (or in what way they learn them). We can, however, disincentivize models from using features that humans definitely don’t use by imposing a prior during training. In our paper, we explore a very simple prior: namely, that imperceptible changes in the input should not cause large changes in the model’s prediction (i.e., models should not rely on brittle features):
\[\begin{equation} \tag{1} \label{eq:robustcond} \|x - x'\|_2 \leq \epsilon \implies \|f(x) - f(x')\| \leq C \cdot \epsilon \end{equation}\]Note that this stability is a necessary, but not sufficient property: all features that humans use certainly obey this property (for reasonably small \(\epsilon\)), but not every feature obeying this property is one that we want our models to rely on.
How should we enforce this prior? Well, observe that the condition $\eqref{eq:robustcond}$ above is actually precisely $\ell_2$-adversarial robustness! Thus, a natural method to employ is robust optimization, which, as we discussed in a previous post, provides reasonable robustness to adversarial perturbations. Concretely, instead of just minimizing loss, we opt to minimize adversarial loss:
\[\min_{\theta} \mathbb{E}_{(x, y) \sim \mathcal{D}} \left[\max_{\delta \in \Delta} L_\theta(x+\delta, y)\right]\]Inverting representations
Now, given a network trained in this manner, what happens if we look for images with the same representations? Concretely, fixing some image $x$, what happens if we look for an image $x’$ that has a matching representation:
\[x' = \arg\min_{x'} \|R(x') - R(x)\|\](Note that we found the image pairs presented earlier for standard networks by solving exactly the above problem.) It turns out that when our model is robust, we end up with an image that is remarkably similar to the original:
Indeed, instead of being able to manipulate feature representations arbitrarily within a small radius, we now find that matching the representation of an image leads to (approximately) matching the image itself.
What can we do with these representations?
We just saw that the learned representation of a robust deep classifier suffices to reconstruct its input pretty accurately (at least in terms of human perception). This highlights two crucial properties of these representations: a) optimizing for closeness in representation space leads to perceptually similar images, b) representations contain a large amount of information about the high-level features of the inputs. These properties are very desirable and prompt us to further explore the structure and potential of these representations. What we find is that the representations of robust networks can truly be thought of as high-level feature representations, and thus (in stark contrast to standard networks) are naturally amenable to various types of manipulation.
In the following sections, we explore these “robust representations” in more depth. A crucial theme in our exploration is model-faithfulness. Though significant work has been done in manipulating and interpreting standard (non-robust) models, it seems as though getting anything meaningful from standard networks requires enforcing priors into the visualization process (see this excerpt “The Enemy of Feature Visualization” for a discussion and illustration of this). This comes at the cost of either hiding vital signals the model utilizes or introducing information that was not already present in the model—thus blurring the line between what information the model actually has, versus what information we introduced when interacting with it. In contrast, throughout our exploration we will rely on only direct optimization over representation space, without introducing any priors or extra information.
Feature visualization
We begin our exploration of robust representations by trying to understand the features captured by their individual components. We visualize these components in the simplest possible way: we perform gradient descent to find inputs that maximally activate individual components of the representation. This is how a few random visualizations look like:

We see a surprising alignment with human concepts. For instance, the last component above seems to correspond to “anemone” and the second-last component to “flowers”. In fact, these names are consistent with the test images maximally activating these neurons—here are the images corresponding to each component:
These visualizations might look familiar. Indeed, similar results have been produced in prior work using non-robust models (e.g. here or here). The difference is that the images above are generated by directly maximizing representation components with gradient descent in input space—we do not enforce any priors or regularization. For standard networks, the same process is unfruitful—to circumvent this, prior work imposes priors on the optimization process.
Feature Manipulation
So far, we have seen that matching the representation of an image starting from random noise, recovers the high-level features of the image itself. At the same time, we saw that individual representation components correspond to high-level human-meaningful concepts. These findings suggests an intriguing possibility: perhaps we can directly modify high-level features of an image by manipulating the corresponding representation over the input space.
This turns out to yield remarkably plausible results! Here we visualize the results of increasing a few select components via gradient descent over the image space for a few random (not cherry-picked) inputs:
These images end up actually exhibiting the relevant features in a way that is plausible to humans (for example, stripes appear mostly on animals instead of the background).
This opens up a wide range of fine-grained manipulations that one can perform by leveraging the learned representations (in fact, stay tuned for some applications in our next blog post).
Input interpolation
In fact, this outlook can be pushed even further—robust models can be leveraged as a tool for another kind of manipulation: input-to-input interpolation. That is, if we think of robust representations as encoding the high-level features of an input in a sensible manner, an intuitive way to interpolate between any two inputs is to linearly interpolate their representations. More precisely, given any two inputs, we can try to construct an interpolation between them by linearly interpolating their representations and then constructing inputs to match these representations.
This rather intuitive way of dealing with representations turns out to work reasonably well—we can interpolate between arbitrary images. Randomly sampled interpolations are shown below:
As we can see, the interpolations appears perceptually plausible. Note that, in contrast to approaches based on generative models (e.g. here or here), this approach can interpolate between arbitrary inputs and not only between those produced by the generative model.
Insight into model predictions
Expanding on our view of deep classifiers as simple linear classifiers on top of the learned representations, there is also a simple way to gain insight into predictions of (robust) models. In particular, for incorrect predictions, we can identify the component most heavily contributing to the incorrect class (in the same way we would for a linear classifier) and then directly manipulate the input to increase the value of that component (with input-space gradient descent). Here we perform this visualization for a few random misclassified inputs:

The resulting images could provide insight into the model’s incorrect decision. For instance, we see the bug becoming a dog eye or negative space becoming the face of a dog. At a high level, these inputs demonstrate which parts of the image the incorrect prediction was most sensitive to.
Still, as a word of caution, it is important to note that just as with all saliency methods (e.g. heatmaps, occlusion studies, etc.), visualizing features and studying misclassification only gives insights into a “local” sense of model behaviour. Deep neural networks are complex, highly non-linear models and it’s important to keep in mind that local sensitivity does not necessarily entail causality.
Towards better learned representations
As we discussed, robust feature representations possess properties that make them desirable from a broader point of view. In particular, we found these representations to be better aligned with a perceptual notion of distance, while allowing us to perform direct input manipulations in a model-faithful way. These are properties that are fundamental to any “truly human-level” representation. One can thus view adversarial robustness as a very potent prior for obtaining representations that are more aligned with human perception beyond the standard goals of security and reliability.
