In a series of two blog posts, we dive into how to build practical certified defenses against adversarial patches. In Part I below, we give an overview of smoothing-based defenses, a popular class of certified defenses, and walk through a specific example of using de-randomized smoothing to defend against adversarial patch attacks. In Part II, we discuss our latest work that demonstrates how using vision transformers with de-randomized smoothing (smoothed ViTs) can significantly improve these defenses. Our approach not only provides better certified defenses against adversarial patches but also maintains standard accuracy and inference times at levels comparable to that of regular (non-robust) models. Thanks to these improvements, smoothed ViTs become a truly viable alternative to regular models.
Adversarial examples are small modifications of inputs that can induce machine learning models to misclassify those inputs. These attacks can be roughly categorized into two broad classes: small, synthetic perturbations that are visually indistinguishable from the original input, and physically realizable attacks that can break deployed machine learning systems in the wild. One popular attack in the latter category, known as adversarial patches, maliciously perturbs a bounded region in the image (typically a square).
 Predicted class: Duck
Predicted class: Duck
 Predicted class: Boat
Predicted class: Boat
Adversarial patches can be used to undermine a variety of vision-based tasks—in particular, have been used to deceive image classifiers, manipulate object detectors, and disrupt optical flow estimation. Such attacks tend to be relatively easy to implement too as they just require, e.g., printing adversarial stickers, creating adversarial pieces of clothing,or manufacturing adversarial glasses.
While several heuristic defenses have been proposed to protect against adversarial patches, some of these defenses were shown to not be fully effective. This is unfortunately a fairly common theme in adversarial examples research.
Certified defenses attempt to alleviate such empirical evaluation problems by providing robustness guarantees that are provable. However, certified guarantees tend to be modest and come at a steep cost. For instance, recently proposed certified defenses against adversarial patches can guarantee only 14% robust accuracy on ImageNet. Furthermore, certified models are often substantially slower (by even 2-4 orders of magnitude) and significantly less accurate (in terms of standard accuracy) than non-robust models, which severely limits their practicality.
Smoothing models for provable robustness
We begin our discussion of certified defenses with an overview of smoothing, a general strategy for creating models that are provably robust to adversarial attacks. They revolve around the idea of deriving a (robust) prediction by aggregating many
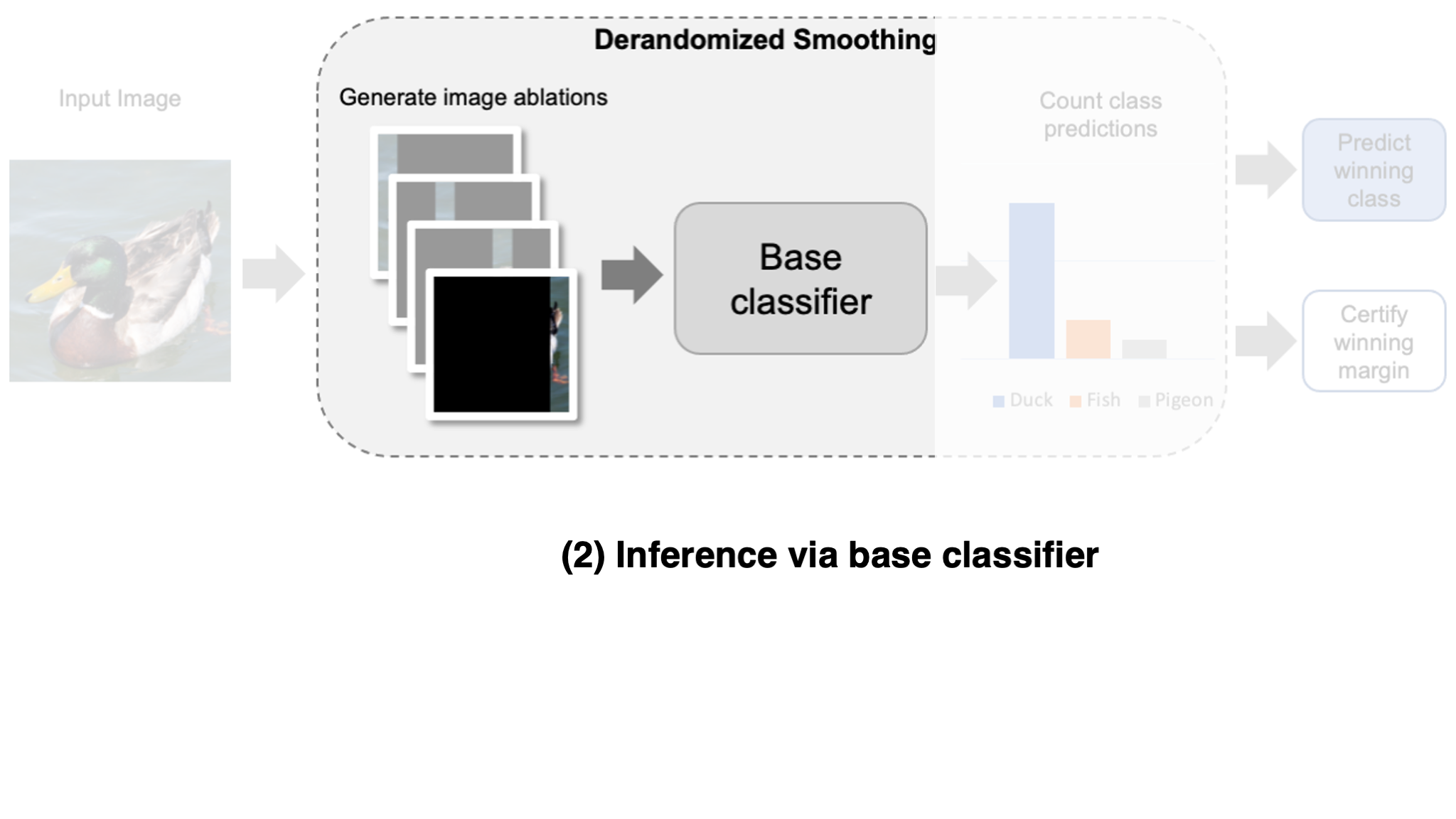
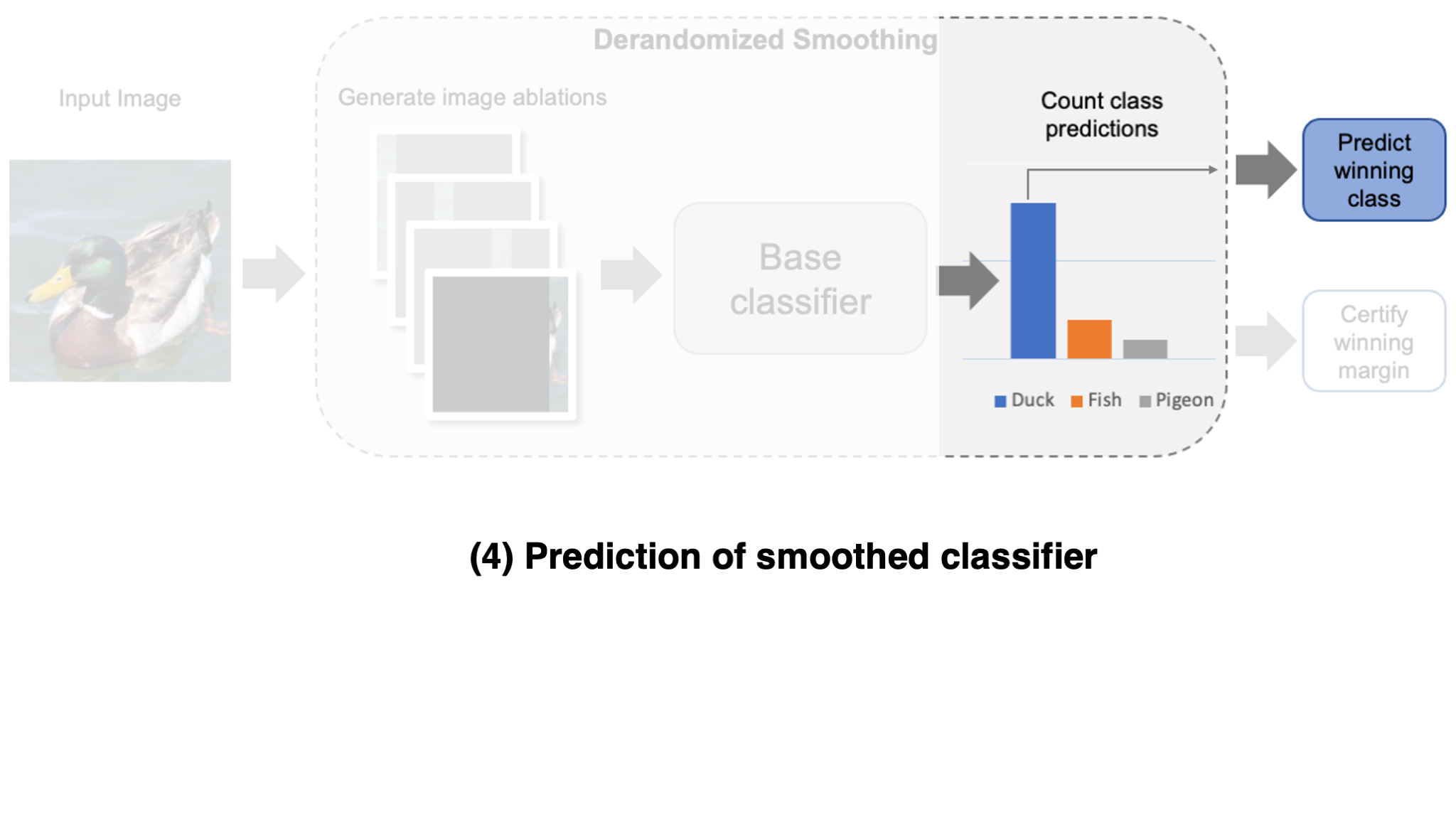
Let’s dive into the details! To create a smoothed classifier, we change the typical forward pass of our classifier (often referred to as the
- Construct variations of the input.
- Classify all input variations individually.
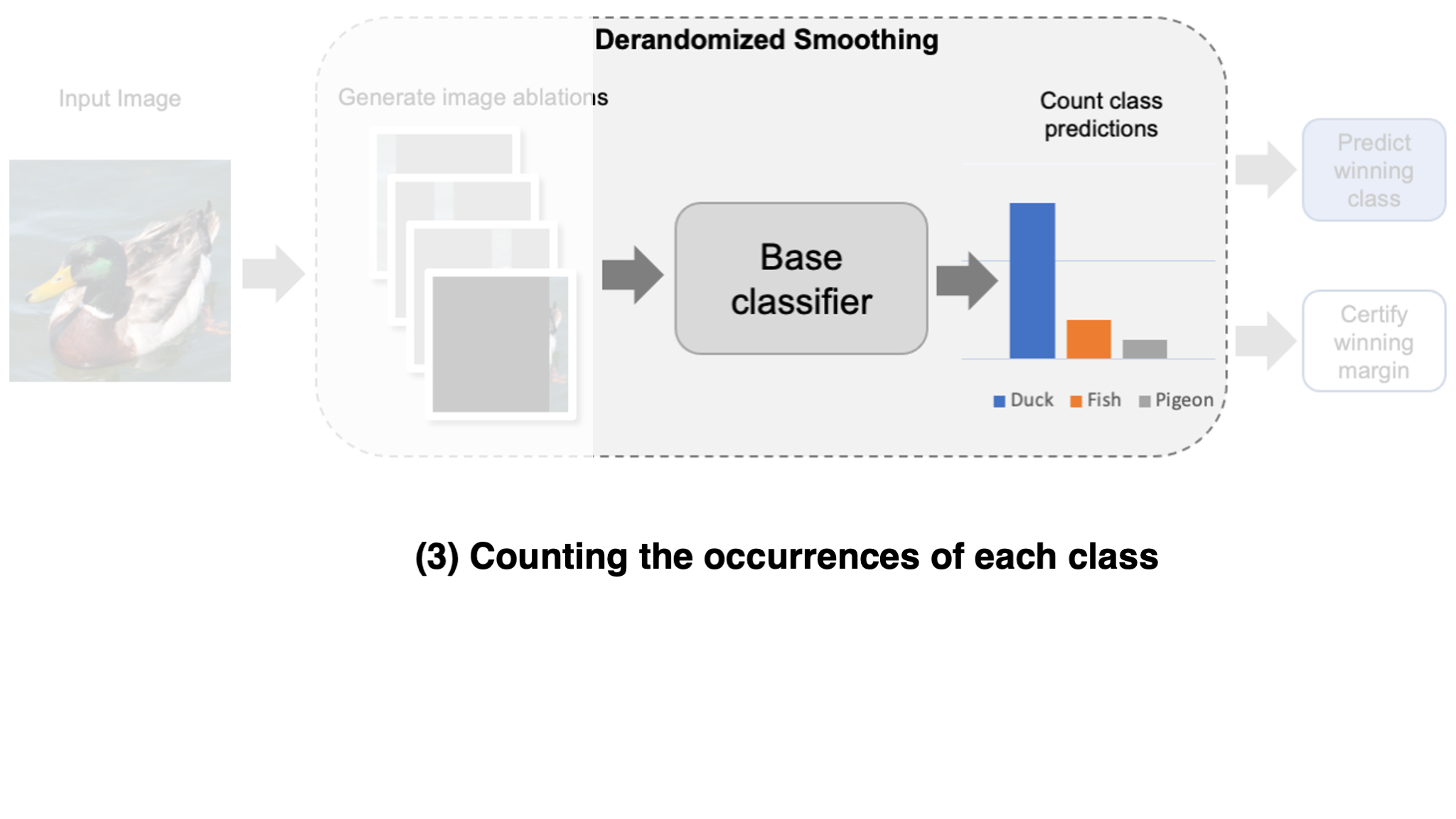
- Output the most frequently predicted class.
Now, once we have such a smoothed classifier, how can we certify its robustness? The key assumption for certification is that an adversary can only affect a limited number of input variations. If this is true, certification amounts to a simple counting problem: if the difference between the first- and second-most frequently predicted classes is larger than what an adversary could ever change via their manipulation, then the prediction is guaranteed to be robust! Importantly, for this approach to work well, it is key that these variations remain informative of the correct class while remaining hard for the adversary to perturb many of them simultaneously. This gives rise to a natural trade-off between robustness and accuracy.
By choosing different types of input variations, smoothing techniques can defend against different types of adversarial attacks. For example, smoothing classifiers with random additive noise can provide certified defenses against adversarial L2 and L1 attacks. On the other hand, smoothing over “pixel flows” can provide certified defenses against Wasserstein perturbations. One can even “smooth” the entire pipeline of both training and inference (treating it as a single module), to get robustness to data poisoning attacks. In general, if we can construct a set of input variations so that the adversary can only affect some fraction of them, we can use smoothing to defend against the corresponding attacks!
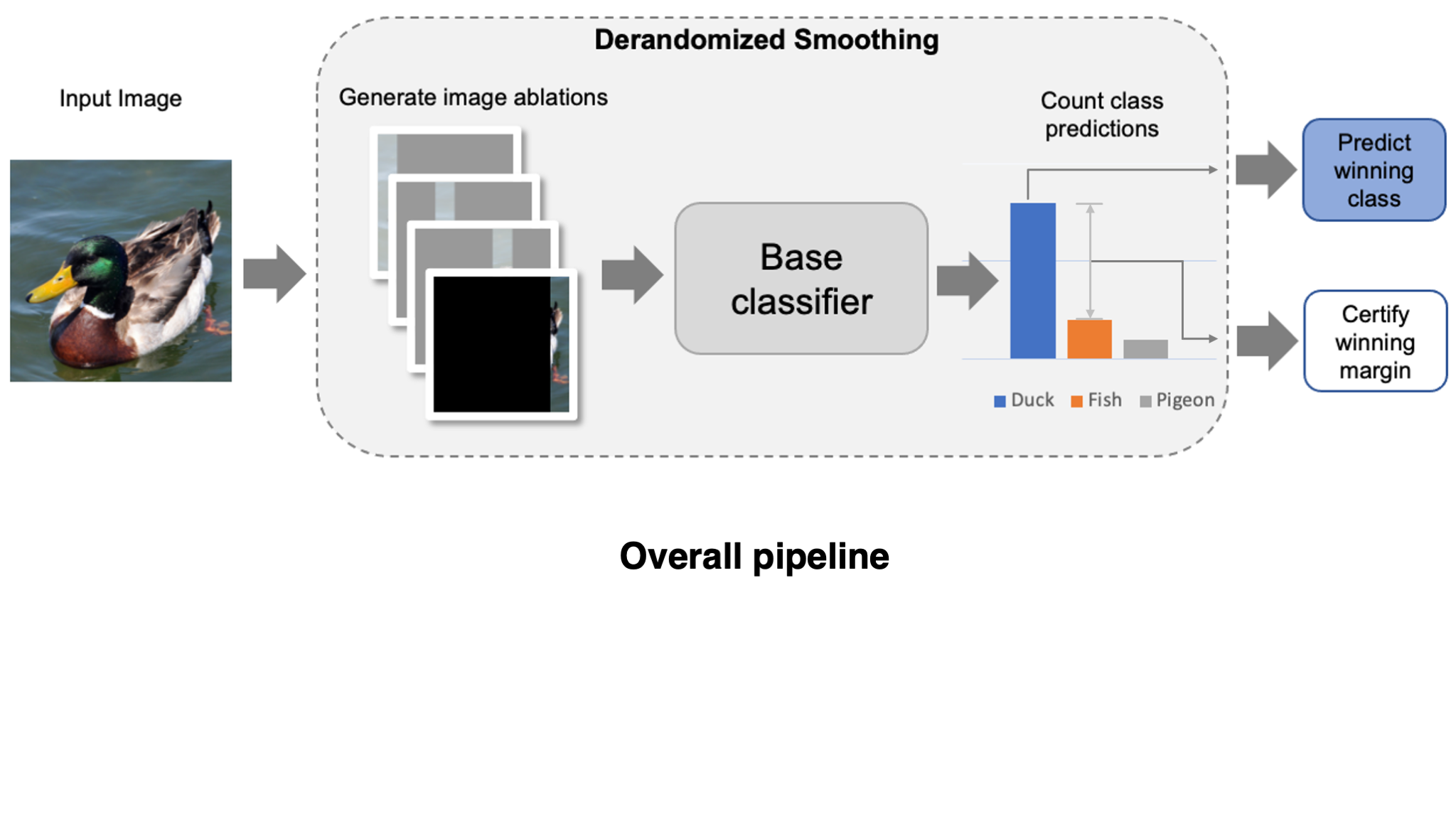
Derandomized Smoothing: A Smoothing Defense against Patch Attacks
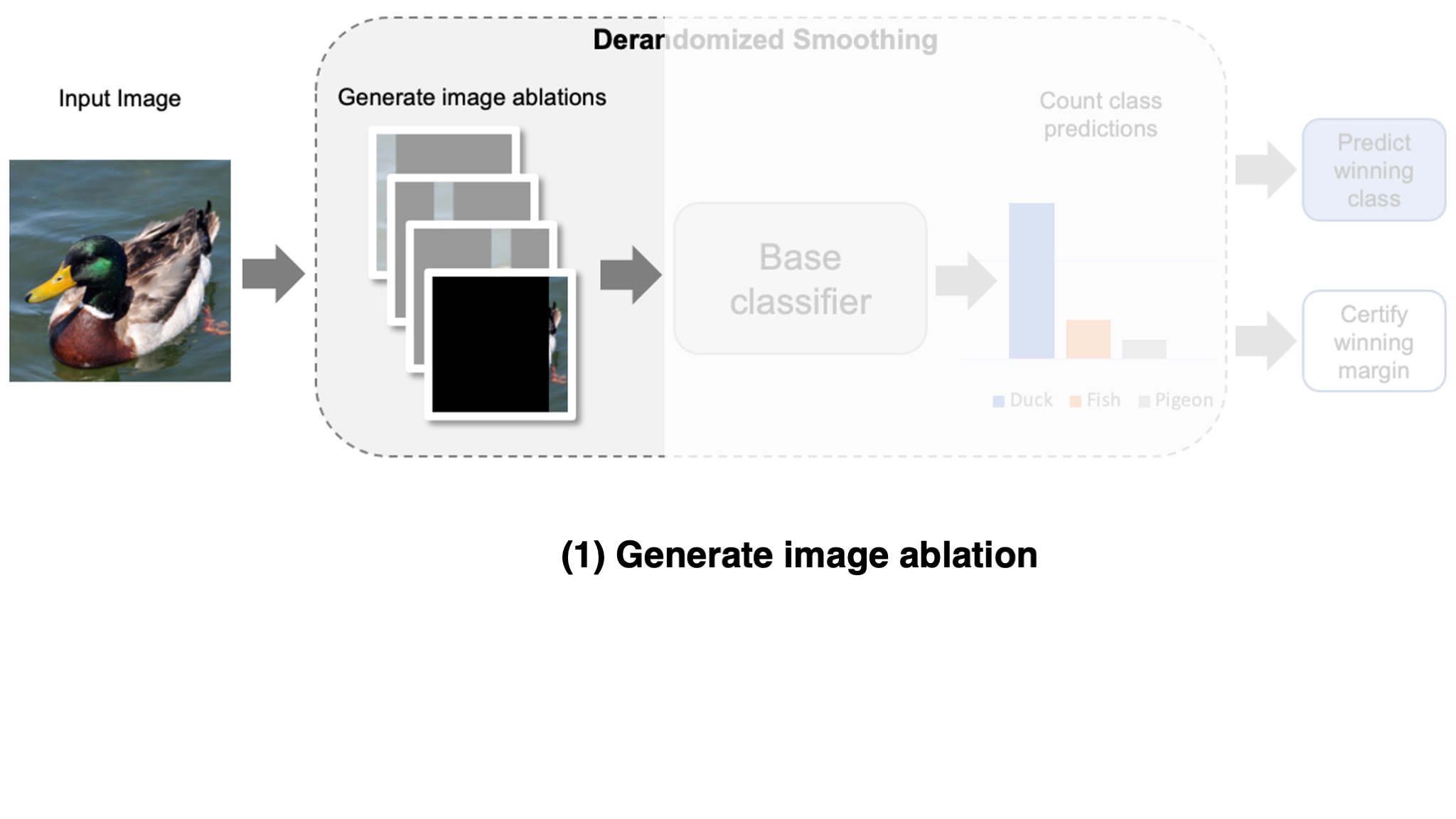
How can we use smoothing to defend against adversarial patches specifically? Recall that to be able to create a smoothing defense, we need to come up with a way to generate variations of an image that limit the effect of an adversarial patch and still be indicative of the correct class label. Here, we exploit a key property of adversarial patches: they are limited to a small, contiguous region of the input image.
Specifically, for each variation, we mask out all of the image except for a small region. In most of these variations, the adversarial patch will be fully masked, and thus cannot affect the model’s prediction by construction. This technique was originally introduced in a certified defense known as derandomized smoothing (Levine & Feizi, 2020). Typically, we leave a column of the image unmasked as shown in the figure below, otherwise known as a column ablation (check out the original paper for some other ablation types).
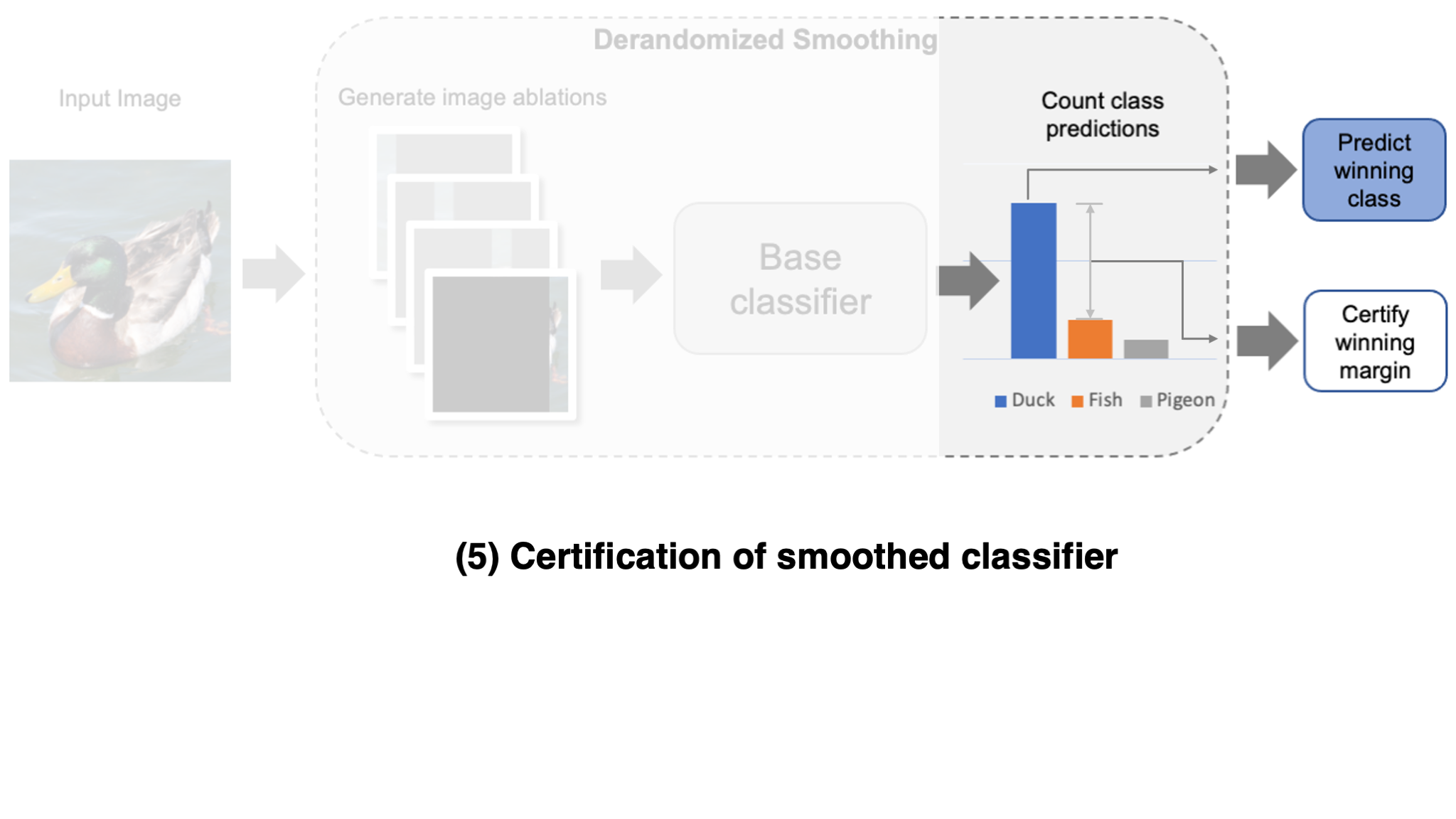
Certified guarantee against patch attacks
Now that we have our smoothed classifier, how can we prove that the prediction is robust to patch attacks? Since a patch is of limited size, an adversary can only affect the few image variations that physically overlap with the patch. Consequently, if the margin of the winning prediction is large enough, then we can guarantee robustness to adversarial patches.
To make this more precise, let $\Delta$ be the number of ablations that a patch could simultaneously affect (in the worst case). If the winning margin is at least $2\Delta$, then the smoothing defense guarantees that the predicted class is robust to this patch size. The fraction of examples which meet this certification threshold is typically referred to as certified accuracy.
Challenges for Certified Patch Defenses
Although certified patch defenses can provide guarantees against adversarial attacks, like many other certified defenses, they face several major challenges that limit their practicality:
- They provide relatively modest guarantees, and can only guarantee robustness for a relatively small fraction of inputs and/or only a small patch size.
- The standard accuracy is typically much lower than that of a standard, non-robust model, forcing on the practitioners an unfavorable “trade-offs” between robustness and accuracy.
- Inference times tend to be several orders of magnitude larger than that of a standard, non-robust model, making certified defenses difficult to deploy in real-time settings.
In the next post, we discuss our latest work on making certified defenses much more practical. Specifically, we show how leveraging vision transformers (ViT) enables better handling of input variations and significant improvement of the margins for certification. With some straightforward modifications to the ViT architecture, we are also able to develop certifiably robust models that not only outperform previous certified defenses but also have practical inference times and standard accuracies.