In our latest paper, in collaboration with Microsoft Research, we explore adversarial robustness as an avenue for training computer vision models with more transferrable features. We find that robust models outperform their standard counterparts on a variety of transfer learning tasks.
What is transfer learning?
Transfer learning is a paradigm where one leverages information from a “source” task to better solve another “target” task. Particularly when there is little training data or compute available for solving the target task, transfer learning provides a simple and efficient way to obtain performant machine learning models.
Transfer learning has already proven its utility in many ML contexts. In natural language processing, for example, one can leverage language models pre-trained on large text corpora to beat state-of-the-art performance on tasks like query answering, entity recognition or part-of-speech classification.
In our work we focus on computer vision; in this context, a standard—and remarkably successful—transfer learning pipeline is “ImageNet pre-training.” This pipeline starts with a deep neural network trained on the ImageNet-1K dataset, and then refines this pre-trained model for a target task. The target task can range from classification of smaller datasets (e.g., CIFAR) to more complex tasks like object detection (e.g., VOC).
Although there are many ways in which one can refine a pre-trained model, we will restrict our attention to the two most popular methods:
- Fixed-feature: In fixed-feature transfer learning, we replace the final (linear) layer of the neural network with a new layer that has the correct number of outputs for the target task. Then, keeping the rest of the layers fixed, we train the newly replaced layer on the target task.
- Full-network: In full-network transfer learning, we also replace the last layer but do not freeze any layers afterwards. Instead, we use the pre-trained network as a sort of “initialization,” and continue training all the layers on the target task.
When at least a moderate amount of data is available, full-network transfer learning typically outperforms the fixed-feature strategy.
How can we improve transfer learning?
Although we don’t have a comprehensive understanding of what makes transfer learning algorithms tick, there has been a long line of work focused on identifying factors that improve (or worsen) performance (examples include [1], [2], [3], [4], [5]).
By design, the pre-trained ImageNet model itself plays a major role here: indeed, a recent study by Kornblith, Shlens, and Le finds that pre-trained models which achieve a higher ImageNet accuracy also perform better when transferred to downstream classification tasks, with a tight linear correspondence between ImageNet accuracy and the accuracy on the target task:
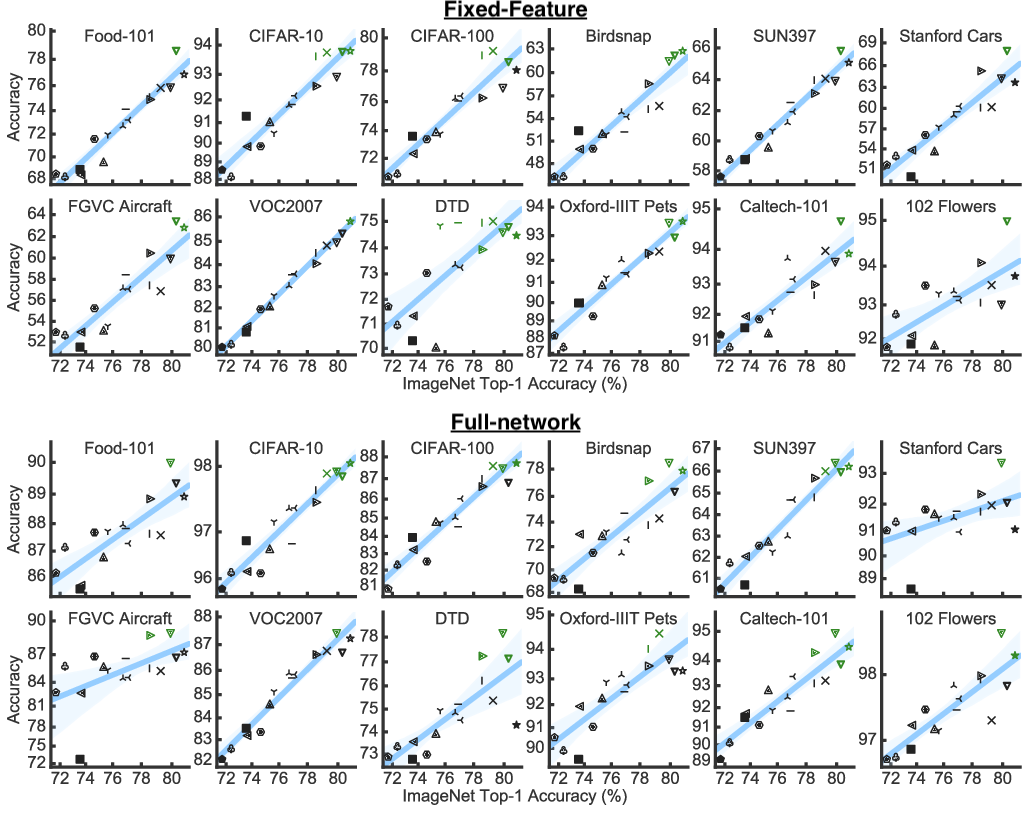
But is improving ImageNet accuracy of the pre-trained model the only way to improve transfer learning performance?
After all, we want to obtain models that have learned broadly applicable features from the source dataset. ImageNet accuracy likely correlates with the quality of features that a model has learned, but may not fully describe the downstream utility of these features. Ultimately, the nature of learned features stems from the priors placed on them during training. For example, there have been studies of the (sometimes implicit) priors imposed by architectural components (e.g., convolutional layers), data augmentation, loss functions and even gradient descent on neural network training.
In our paper, we study another prior: adversarial robustness. Adversarial robustness—a rather frequent subject on this blog—refers to model’s invariance to small (often imperceptible) perturbations of natural inputs, called adversarial examples.
Standard neural networks (i.e., trained with the goal of maximizing accuracy) are extremely vulnerable to such adversarial examples. For example, with just a tiny perturbation to the pig image below, a pre-trained ImageNet classifier will predict it as an “airliner” with 99% confidence:
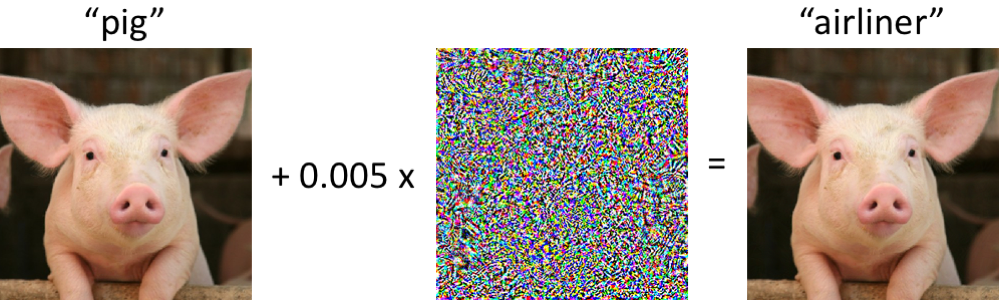
Adversarial robustness is thus typically induced at training time by replacing the standard loss minimization objective with a robust optimization objective (see our post on robust optimization for more background):
\[\min_{\theta}\ \mathbb{E}_{(x,y)\sim D}\left[\mathcal{L}(x,y;\theta)\right] \implies \min_{\theta}\ \mathbb{E}_{(x,y)\sim D} \left[\max_{\|\delta\|_2 \leq \varepsilon} \mathcal{L}(x+\delta,y;\theta) \right].\]The above objective trains models to be robust to image perturbations that are
small in (pixel-wise) $\ell_2$ (Euclidean)
[A quick plug: Our robustness Python library, used for the code release of this paper, enables one to easily train and manipulate both standard and adversarially robust models.]
Although adversarial robustness has been initially studied solely through the lens of machine learning security, a line of recent work (including some that’s been previously covered on this blog) has begun to study adversarially robust models in their own right, framing adversarial robustness as a prior that forces models to learn features that are locally stable. These works have found that on the one hand, adversarially robust models tend to attain lower accuracy than their standardly-trained counterparts.
On the other hand, recent work suggests that the feature representations of robust models carry several advantages over those of standard models, such as better-behaved gradients, representation invertibility, and more specialized features. We’ve actually discussed some of these observations in earlier posts on this blog—see, e.g., our posts about representation learning and image synthesis.
These desirable properties might suggest that robust neural networks are learning better feature representations than standard networks, which could improve transfer performance.
Adversarial robustness and transfer learning
So in summary, we have standard models with high accuracy on the source task but little (or no) robustness; and we have adversarially robust models, which are worse in terms of ImageNet accuracy, but have the “nice” representational properties identified and discussed by prior works. Which models are better for transfer learning?
To answer this question, we trained and examined a large collection of standard and robust ImageNet models, while grid searching over a wide range of hyperparameters and architectures to find the best model of each type. (All models are available for download via our code/model release and more details on our training procedure can be found there and in our paper). We then performed transfer learning (using both fixed-feature and full-network refinement) from each trained model to 12 downstream classification tasks.
It turns out that adversarially robust source models fairly consistently outperform their standard counterparts in terms of downstream accuracy. In the table below, we compare the accuracies of the best standard model (searching over hyperparameters and architecture) and the best robust model (searching over the previous factors as well as robustness level $\varepsilon$):
This difference in performance tends to be particularly striking in the context of fixed-feature transfer learning. The following graph shows, for each architecture and downstream classification task, the best standard model compared to the best robust model in that setting. As we can see, adversarially robust models improve on the performance of their standard counterparts, and the gap tends to increase as networks increase in width:
Adversarial robustness improved downstream transfer performance even when the target task was not a classification one. For example, the following table compares standard and robust pre-training for use in downstream object detection and instance segmentation:
Robustness versus accuracy
So it seems like robust models, despite being less accurate on the source task, are actually better for transfer learning purposes. Indeed, the linear relation between ImageNet accuracy and transfer performance observed in prior work (see our discussion above) doesn’t seem to hold when the robustness parameter is varied. Compare the graphs below to the ones at the very start of this post:
How do we reconcile our observations with these trends observed by prior work?
We hypothesize that robustness and accuracy have disentangled effects on transfer performance. That is, for a fixed level of robustness, higher accuracy on the source task helps transfer, and for a fixed level of accuracy, increased robustness helps transfer. Indeed, as shown below, for a fixed level of robustness, the accuracy-transfer relation tends to hold strongly:
In addition to reconciling our results with those of prior work, these findings suggest that ongoing work on developing more accurate robust models may have the added benefit of further improving transfer learning performance.
Other empirical mysteries and future work
This post discussed how adversarially robust models might constitute a promising avenue for improving transfer learning, and already often outperform standard models in terms of downstream accuracy. In our paper, we study this phenomenon more closely: for example, we examine the effects of model width, and we compare adversarial robustness to other notions of robustness. We also uncover a few somewhat mysterious properties: for example, resizing images seems to have a non-trivial effect on the relationship between robustness and downstream accuracy.
Finally, while our work provides evidence that adversarially robust computer vision models transfer better, understanding precisely why this is the case remains open. More broadly, the results we observe indicate that we still do not yet fully understand (even empirically) the ingredients that make transfer learning successful. We hope that our work prompts an inquiry into the underpinnings of modern transfer learning.
