In our new paper, we take a closer look at the design space of so-called feature priors—i.e., priors that bias the features that a model relies on. We show that models trained with diverse sets of such priors have less overlapping failure modes and can correct each other’s mistakes.
At the core of deep learning’s success is its ability to automatically learn useful features from raw data, e.g., image pixels. Consequently, the set of such learned features has a large impact on the deep learning model’s ability to generalize, especially when the deployment conditions deviate from the training environment. For example, a model that relies heavily on the background of an image may have trouble recognizing a cow on a beach if during training it was mostly encountering cows on grass.
So, how can one control the features that a model relies on? This is often accomplished by changing the model’s architecture or training methodology. For example, by choosing to use a convolutional neural network a model designer biases that model towards learning a hierarchy of spatial features. Similarly, by employing data augmentation during training, one biases the model towards features that are invariant to the particular augmentations used. In fact, researchers have recently explored explicitly manipulating the set of features that a model learns, via, for example, suppressing texture information by training on stylized inputs or by training with worst-case input perturbations to avoid brittle features.
Now, all of these design choices can be thought of as imposing feature priors, i.e., biasing a model towards learning a particular type of features. The question thus becomes: how can we explore and leverage this space of feature priors in a more systematic and purposeful manner?
Feature Priors as Distinct Perspectives on Data
The core idea is to view different feature priors as distinct perspectives on the data. That is, since different sets of features are likely to generalize differently across inputs, by considering multiple such sets in tandem we can obtain a more holistic (and thus, hopefully, reliable) view on our data.
Setting up our case study: Let us focus our attention on two concrete feature priors: shape and texture. These two priors arise naturally in the context of image classification and will serve as the basis of our study. We impose these priors through deliberate construction of the dataset and architecture:
- Shape-based priors: We remove texture information from the images with the help of an edge detection algorithm. We use for this purpose two canonical edge detection algorithms from the computer vision literature: Canny and Sobel.
- Texture-based priors: We use a variant of the BagNet model, which limits the model’s receptive field to prevent the model from relying on global structures like shape.
 Original
Original
 Sobel
Sobel
 Canny
Canny
 BagNet
BagNet
Intuitively, these priors should correspond to very different sets of features. But are the views offered by these priors truly complementary? A simple way to measure this is to quantify the overlap of the failure modes of the models trained with the respective priors. Specifically, we measure the correlation of predicting the correct label for each pair of such models. We perform this analysis on a subset of CIFAR-10.
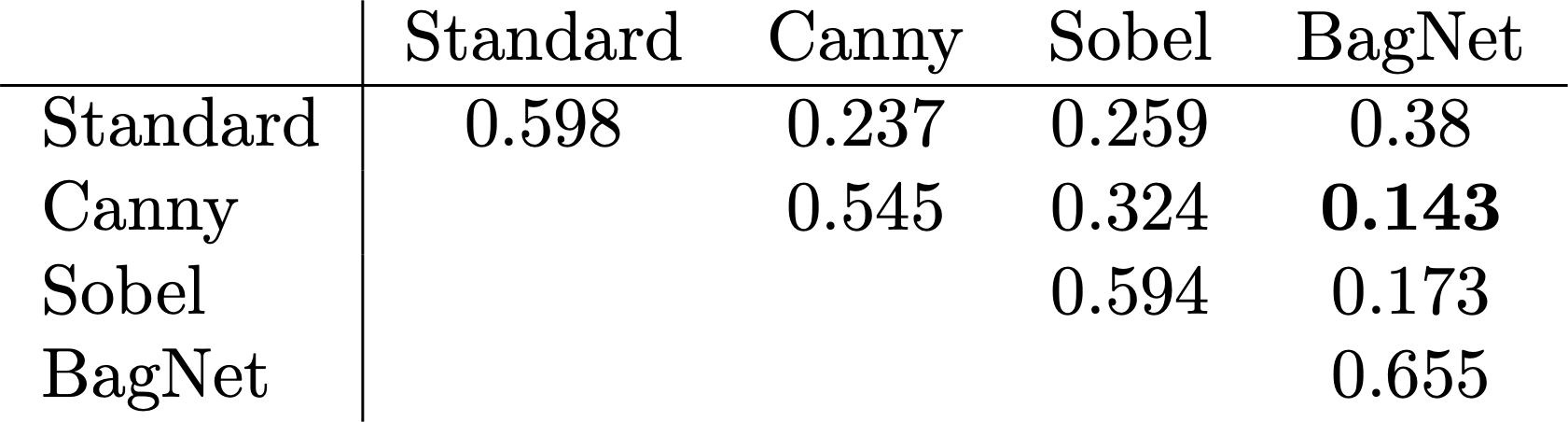
It looks like these results match our intuition! Indeed, models corresponding to the same feature priors (but different random initialization) are relatively well correlated with each other. This also includes the case when we use two different shape biases. On the other hand, when we consider a pairing of a shape-biased model and a texture-biased model the predictions are the least correlated, that is, they make different mistakes on the test set.
Combining feature priors
Since shape- and texture-biased models make different types of mistakes, can we leverage their diversity to improve our predictions?
Ensembles
A natural way to examine that question is combining these models in an ensemble. This ensemble, for a given test input, evaluates both models on that input and then outputs the one prediction that is assigned the highest probability by the respective model. It turns out that, indeed, such an ensemble is significantly more accurate when we combine in this way models with different priors (as opposed to combining two models trained with the same prior, but with different initializations). Clearly, prediction diversity matters!
Co-Training
So far, we demonstrated that models with diverse feature priors have less overlapping failure modes, and can be combined via ensembling for improved generalization performance. However, is that all? In particular, are there ways of incorporating prior diversity during training (as opposed to ensembling post hoc) in order to improve the learning process itself?
To answer this question, we focus on self-training, a methodology often employed when the labeled data is insufficient to learn a well-generalizing model alone, but a large pool of unlabeled data is available. The key idea in self-training is to use a model trained on the labeled data to produce “pseudo-labels” for the unlabeled data and then use these labels for further training. This setting is particularly challenging since: (a) the (original) labelled data points are typically too few to learn reliable prediction rules, and (b) any incorrect prediction rules learned will be reinforced via pseudo-labelling (so-called “confirmation bias”).
From this perspective, our goal is to jointly train models with different feature priors to mitigate the propagation of such incorrect prediction rules. We will do so by leveraging the well-established framework of co-training, a framework designed for learning from data with multiple independent sets of features. In the context of our study, we can instantiate this framework as follows.
First, we train one model for each prior using the labeled data. Then, we use each of these models to pseudo-label the unlabelled data and add the examples which are assigned the highest predicted probability to a joint pseudo-labelled data pool. We then use these examples to train both models further and keep repeating this process until we eventually use all the unlabeled data for training. In the end, we combine these models into a single classifier by training a standard model from scratch on the combined pseudo-labels.
The intuition behind this process is that by jointly training models which rely on different features, these models can learn from each other’s predictions. If one model produces incorrect pseudo-labels, we can hope that the other model will correct them by relying on alternative prediction rules.
So, how well does this approach work? To evaluate it, we extract from the CIFAR-10 dataset a small, labeled part (100 examples per class) and treat the rest of this dataset unlabeled. We then compare how different training methods—specifically, self-training a model with a single prior, and co-training models with different priors—perform in this setting. (For an additional baseline, we also consider ensembling two such models with different priors together.)
Overall, we find that co-training with shape- and texture-based priors can significantly improve the test accuracy of the final model compared to self-training with any of the priors alone. In fact, co-training models with diverse priors also improves significantly upon simply combining self-trained models in an ensemble. So these models are indeed able to take advantage of each other’s predictions during training.
Priors and Spurious Correlations
So far, we were focused on a setting where the training and test data were all sourced from the same distribution. However, a major challenge for the real-world model deployment are spurious correlations: associations which are predictive on the training data but not valid for the actual task. For example, an image classification model may predict an object’s class based on its location, or rely on artifacts of the data collection process.
How can we train models that avoid picking up such spurious correlations? For this problem to be tractable in the first place, we need to rely on some information beyond the training data. Here, we will assume that we have access to an unlabelled dataset where this correlation does not hold (e.g., cows do not always appear on grass and thus the correlation “grass”->”cow” is not always predictive). This is a rather mild assumption in settings where we can easily collect unlabelled data from a variety of sources—if a correlation is spurious, it is less likely to be uniformly present.
As a concrete example, let us consider a simple gender classification task based on the CelebA dataset. In this task, we will introduce a spurious correlation into the labeled data by only collecting photographs of blond females and non-blond males. This makes hair color a good predictor of gender for the labeled dataset, but will not generalize well beyond that as such correlation does not hold in the real world.
Our goal here will be to harness an unbiased, yet unlabelled dataset, to learn a model that avoids this correlation. We will again attempt to do so by co-training models with diverse feature priors: shape and texture. Notice that since the spurious correlation is color-based, shape-biased models are likely to ignore it. As a result, we anticipate that the prediction of the shape-biased and texture-biased models will differ on inputs where hair color disagrees with gender. Thus, during co-training, these models are intuitively providing each other with counter-examples and are thus likely to steer each other away from incorrect prediction rules.
We find that this is indeed the case! When we co-train a texture-biased model with a shape-biased one, the texture-biased model improves substantially, relying less on the hair color. Moreover, the shape-biased model also improves through co-training. This indicates that even though the texture-biased model relies heavily on the spurious correlation, it also captures non-spurious associations that, through pseudo-labeling, are useful for the shape-based model too.
Outlook: Exploring the Design Space of Priors
In this post, we described how models trained with diverse feature priors can be leveraged during training to learn more reliable prediction rules (e.g., in the presence of spurious correlations). However, we view our exploration as only the first step in systematically exploring the design space of feature priors. We believe that this direction will yield an important building block of reliable training and deployment pipelines.
